《中考數(shù)學(xué)培優(yōu)復(fù)習(xí) 第13課時(shí) 二次函數(shù)及其應(yīng)用》由會(huì)員分享���,可在線閱讀���,更多相關(guān)《中考數(shù)學(xué)培優(yōu)復(fù)習(xí) 第13課時(shí) 二次函數(shù)及其應(yīng)用(4頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�����。
1、中考數(shù)學(xué)培優(yōu)復(fù)習(xí) 第13課時(shí) 二次函數(shù)及其應(yīng)用
一�����、【知識(shí)要點(diǎn)】
1. 二次函數(shù)的解析式:(1)一般式: ;(2)頂點(diǎn)式: ��;
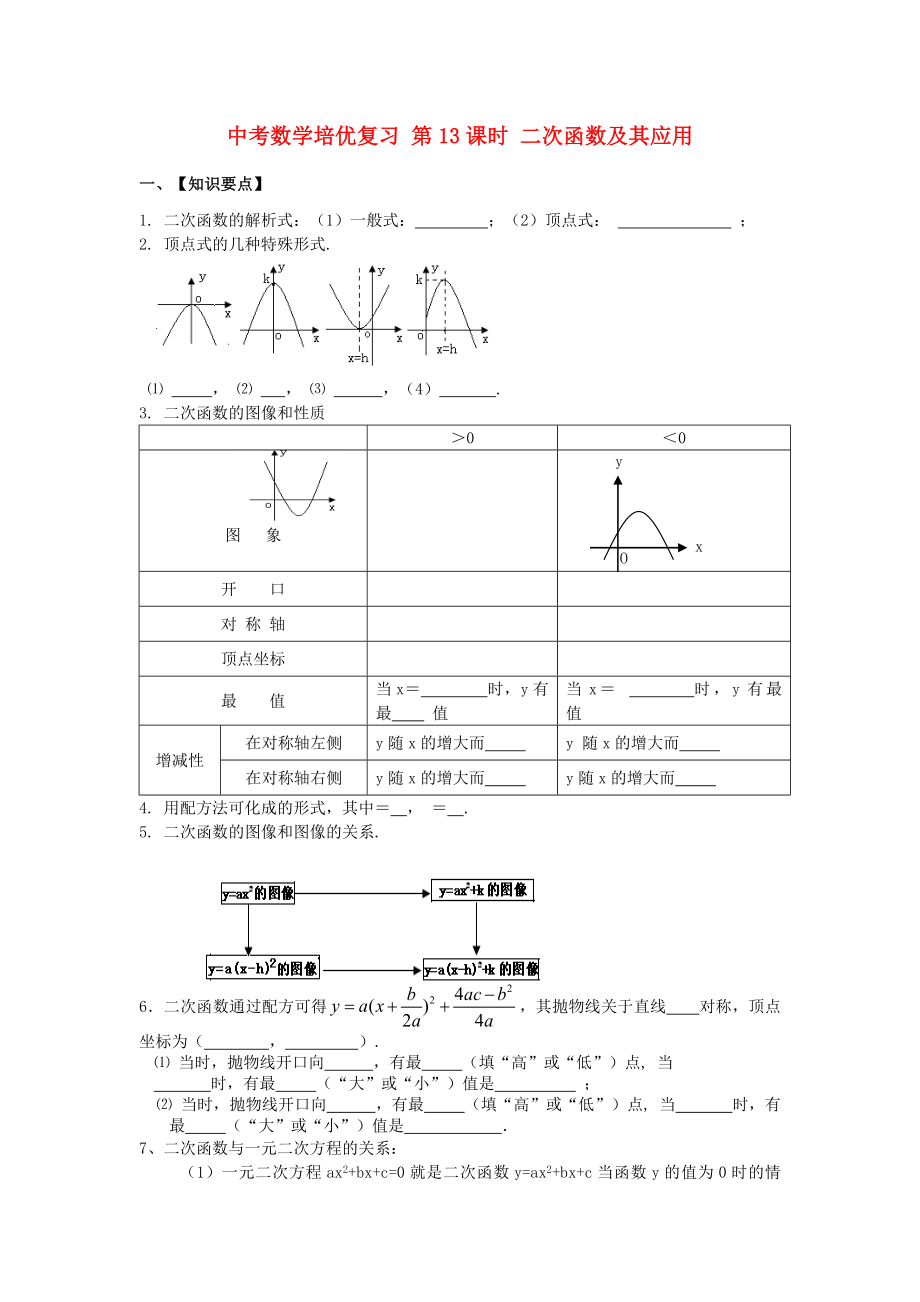
2. 頂點(diǎn)式的幾種特殊形式.
⑴ ��, ⑵ ���, ⑶ ,(4) .
3. 二次函數(shù)的圖像和性質(zhì)
>0
y
x
O
<0
圖 象
開 口
對(duì) 稱 軸
頂點(diǎn)坐標(biāo)
最 值
當(dāng)x= 時(shí)�����,y有最 值
當(dāng)x= 時(shí),y有最
2�、 值
增減性
在對(duì)稱軸左側(cè)
y隨x的增大而
y 隨x的增大而
在對(duì)稱軸右側(cè)
y隨x的增大而
y隨x的增大而
4. 用配方法可化成的形式��,其中= ��, = .
5. 二次函數(shù)的圖像和圖像的關(guān)系.
6.二次函數(shù)通過配方可得�����,其拋物線關(guān)于直線 對(duì)稱�����,頂點(diǎn)坐標(biāo)為( ��, ).
⑴ 當(dāng)時(shí)��,拋物線開口向 ,有最 (填“高”或“低”)點(diǎn), 當(dāng)
時(shí)�����,有最 (“大”或“小”)值是 ��;
⑵ 當(dāng)時(shí)��,拋物線開口向 ��,有最
3�����、(填“高”或“低”)點(diǎn), 當(dāng) 時(shí)���,有最 (“大”或“小”)值是 .
7���、二次函數(shù)與一元二次方程的關(guān)系:
(1)一元二次方程ax2+bx+c=0就是二次函數(shù)y=ax2+bx+c當(dāng)函數(shù)y的值為0時(shí)的情況.
(2)二次函數(shù)y=ax2+bx+c的圖象與x軸的交點(diǎn)有三種情況:有兩個(gè)交點(diǎn)、有一個(gè)交點(diǎn)���、沒有交點(diǎn)���;當(dāng)二次函數(shù)y=ax2+bx+c的圖象與x軸有交點(diǎn)時(shí)�,交點(diǎn)的橫坐標(biāo)就是當(dāng)y=0時(shí)自變量x的值��,即一元二次方程ax2+bx+c=0的根.
(3)當(dāng)二次函數(shù)y=ax2+bx+c的圖象與 x軸有兩個(gè)交點(diǎn)時(shí)�����,則一元二次方程y=ax
4、2+bx+c有兩個(gè)不相等的實(shí)數(shù)根�;當(dāng)二次函數(shù)y=ax2+bx+c的圖象與x軸有一個(gè)交點(diǎn)時(shí)�����,則一元二次方程ax2+bx+c=0有兩個(gè)相等的實(shí)數(shù)根����;當(dāng)二次函數(shù)y=ax2+ bx+c的圖象與 x軸沒有交點(diǎn)時(shí)��,則一元二次方程y=ax2+bx+c沒有實(shí)數(shù)根
8��、二次函數(shù)的應(yīng)用:
(1)二次函數(shù)常用來解決最優(yōu)化問題�,這類問題實(shí)際上就是求函數(shù)的最大(?���。┲?���;
(2)二次函數(shù)的應(yīng)用包括以下方面:分析和表示不同背景下實(shí)際問題中變量之間的二次函數(shù)關(guān)系�����;運(yùn)用二次函數(shù)的知識(shí)解決實(shí)際問題中的最大(?��。┲担?
二��、【經(jīng)典例題剖析】
1. 已知二次函數(shù)y=x2-6x+8����,求:
(1)拋
5����、物線與x軸J軸相交的交點(diǎn)坐標(biāo)���;
(2)拋物線的頂點(diǎn)坐標(biāo);
(3)畫出此拋物線圖象����,利用圖象回答下列問題:
①方程x2 -6x+8=0的解是什么��?
②x取什么值時(shí)���,函數(shù)值大于0�?
③x取什么值時(shí),函數(shù)值小于0��?
2. 已知拋物線y=x2-2x-8��,
(1)求證:該拋物線與x軸一定有兩個(gè)交點(diǎn)���;
(2)若該拋物線與x軸的兩個(gè)交點(diǎn)分別為A���、B�����,且它的頂點(diǎn)為P�,求△ABP的面積.
3.如圖所示���,直線y=-2x+2與軸�����、軸分別交于點(diǎn)A、B����,以線段AB為直角邊在第一象限內(nèi)作等腰直角△ABC��,∠BAC=90
6、o��,
過C作CD⊥軸,垂足為D
(1)求點(diǎn)A��、B的坐標(biāo)和AD的長(zhǎng)
(2)求過B ��、A、D三點(diǎn)的拋物線的解析式
三�����、當(dāng)堂檢測(cè)
一�����、選擇題
1.(xx·濱州)下列函數(shù)中,圖象經(jīng)過原點(diǎn)的是( )
A.y=3x B.y=1-2x
C.y= D.y=x2-1
2.(xx·成都)將二次函數(shù)y=x2-2x+3化為y=(x-h(huán))2+k的形式�,結(jié)果為( )
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+2
3.(xx·黃石)二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖����,則函數(shù)值y>0時(shí)
7����、����,x的取值范圍是( )
A.x<-1 B.x>3
C.-1<x<3 D.x<-1或x>3
4.(xx·畢節(jié))拋物線y=2x2,y=-2x2,y=x2共有的性質(zhì)是( )
A.開口向下 B.對(duì)稱軸是y軸
C.都有最低點(diǎn) D.y隨x的增大而減小
5.(xx·荊門)將拋物線y=x2-6x+5向上平移2個(gè)單位長(zhǎng)度���,再向右平移1個(gè)單位長(zhǎng)度后,得到的拋物線解析式是( )
A.y=(x-4)2-6 B.y=(x-4)2-2
C.y=(x-2)2-2 D.y=(x-1)2-3
6.(xx·陜西)二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖����,則下
8��、列結(jié)論中正確的是( )
A.c>-1 B.b>0
C.2a+b≠0 D.9a+c>3b
7.(xx·云南)拋物線y=x2-2x+3的頂點(diǎn)坐標(biāo)是__ _.
8.已知二次函數(shù)的圖象開口向上���,且頂點(diǎn)在y軸的負(fù)半軸上�����,請(qǐng)你寫出一個(gè)滿足條件的二次函數(shù)的表達(dá)式_ _ _.
9.(xx·揚(yáng)州)如圖���,拋物線y=ax2+bx+c(a>0)的對(duì)稱軸是過點(diǎn)(1�����,0)且平行于y軸的直線��,若點(diǎn)P(4�,0)在該拋物線上����,則4a-2b+c的值為__ __.
10.出售某種文具盒,若每個(gè)獲利x元����,一天可售出(
9���、6-x)個(gè)����,則當(dāng)x=__ __元時(shí)���,一天出售該種文具盒的總利潤(rùn)y最大.
11.?dāng)?shù)學(xué)課本上���,用“描點(diǎn)法”畫二次函數(shù)y=ax2+bx+c的圖象時(shí)��,列了如下表格:
x
…
-1
-2
0
1
2
…
y
…
-6
-4
-2
-2
-2
…
根據(jù)表格上的信息回答問題:該二次函數(shù)y=ax2+bx+c在x=3時(shí)���,y=__ __.
12.(xx·菏澤)如圖��,平行于x軸的直線AC分別交拋物線y1=x2(x≥0)與y2=(x≥0)于B�,C兩點(diǎn)�,過點(diǎn)C作y軸的平行線交y1于點(diǎn)D,直線DE∥AC����,交y2于點(diǎn)E,則=_
三����、解答題
13.(xx·濱州
10��、)已知二次函數(shù)y=x2-4x+3.
(1)用配方法求其圖象的頂點(diǎn)C的坐標(biāo)�,并描述該函數(shù)的函數(shù)值隨自變量的增減而變化的情況�����;
(2)求函數(shù)圖象與x軸的交點(diǎn)A����,B的坐標(biāo)��,及△ABC的面積.
14.(xx·泉州)如圖�,已知二次函數(shù)y=a(x-h(huán))2+的圖象經(jīng)過原點(diǎn)O(0,0)�,A(2,0).
(1)寫出該函數(shù)圖象的對(duì)稱軸�����;
(2)若將線段OA繞點(diǎn)O逆時(shí)針旋轉(zhuǎn)60°到OA′,試判斷點(diǎn)A′是否為該函數(shù)圖象的頂點(diǎn)�����?
16.(xx·泰州)某研究所將某種材料加熱到1000 ℃時(shí)停止加熱,并立即將材料分為A�����,B兩組�,采用不同工藝做降溫對(duì)比實(shí)驗(yàn)�,設(shè)降溫開始后經(jīng)過x min時(shí),A�����,B兩組材料的溫度分別為yA℃,yB℃���,yA���,yB與x的函數(shù)關(guān)系式分別為yA=kx+b,yB=(x-60)2+m(部分圖象如圖所示)�����,當(dāng)x=40時(shí)��,兩組材料的溫度相同.
(1)分別求yA�����,yB關(guān)于x的函數(shù)關(guān)系式��;
(2)當(dāng)A組材料的溫度降至120℃時(shí)�����,B組材料的溫度是多少?
(3)在0<x<40的什么時(shí)刻����,兩組材料溫差最大�?
 中考數(shù)學(xué)培優(yōu)復(fù)習(xí) 第13課時(shí) 二次函數(shù)及其應(yīng)用
中考數(shù)學(xué)培優(yōu)復(fù)習(xí) 第13課時(shí) 二次函數(shù)及其應(yīng)用