《2022年高考數(shù)學(xué)一輪復(fù)習(xí) 第一講 空間幾何體習(xí)題 理 新人教A版》由會員分享，可在線閱讀，更多相關(guān)《2022年高考數(shù)學(xué)一輪復(fù)習(xí) 第一講 空間幾何體習(xí)題 理 新人教A版（4頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

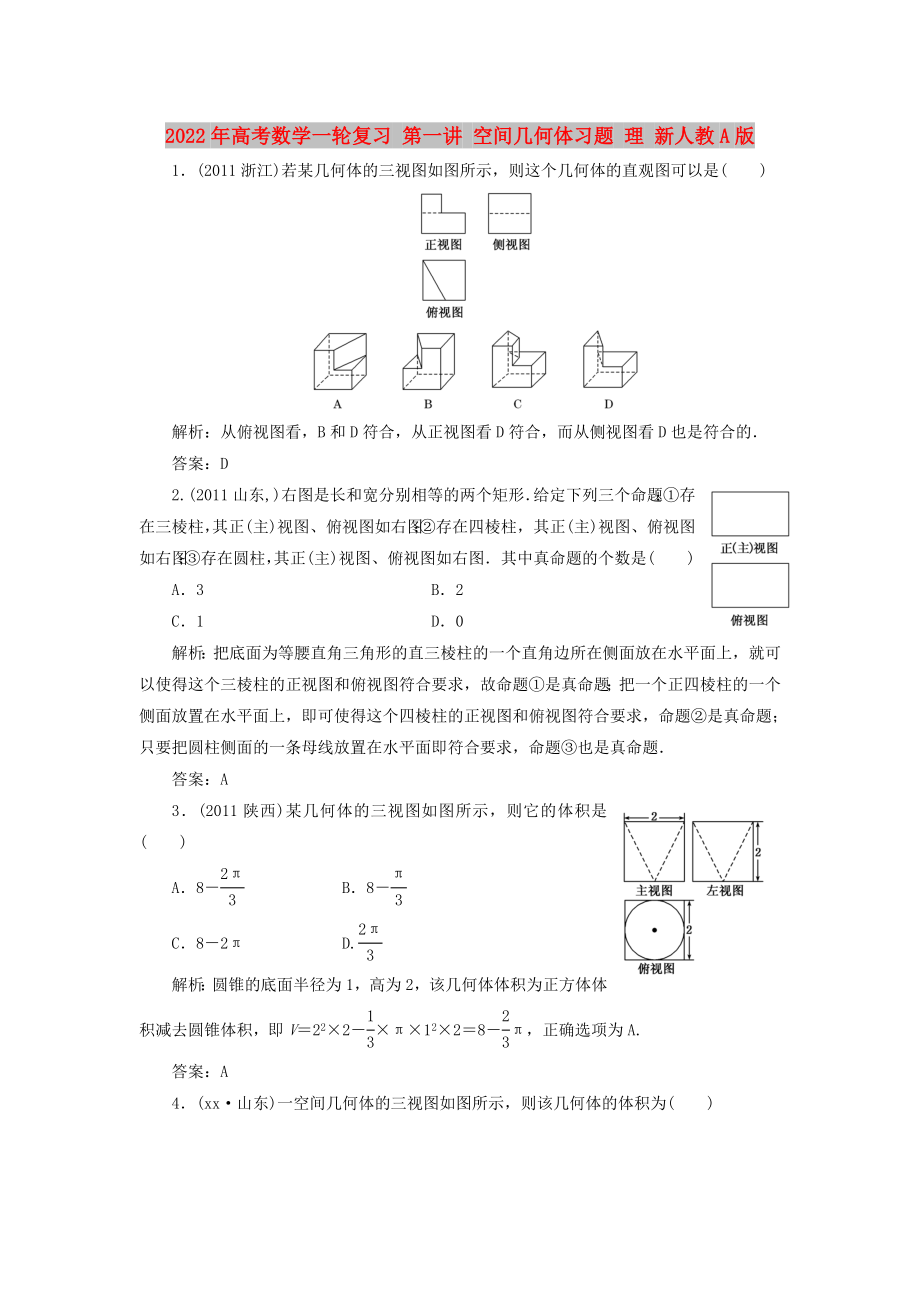
1、2022年高考數(shù)學(xué)一輪復(fù)習(xí) 第一講 空間幾何體習(xí)題 理 新人教A版 1．(2011浙江)若某幾何體的三視圖如圖所示，則這個幾何體的直觀圖可以是(　　) 解析：從俯視圖看，B和D符合，從正視圖看D符合，而從側(cè)視圖看D也是符合的． 答案：D 2.(2011山東,)右圖是長和寬分別相等的兩個矩形．給定下列三個命題：①存在三棱柱，其正(主)視圖、俯視圖如右圖；②存在四棱柱，其正(主)視圖、俯視圖如右圖；③存在圓柱，其正(主)視圖、俯視圖如右圖．其中真命題的個數(shù)是(　　) A．3　　　　　　　　　　 B．2 C．1 D．0 解析：把底面為等腰直角三角形的直三棱柱的一個直角邊所在

2、側(cè)面放在水平面上，就可以使得這個三棱柱的正視圖和俯視圖符合要求，故命題①是真命題；把一個正四棱柱的一個側(cè)面放置在水平面上，即可使得這個四棱柱的正視圖和俯視圖符合要求，命題②是真命題；只要把圓柱側(cè)面的一條母線放置在水平面即符合要求，命題③也是真命題． 答案：A 3．(2011陜西)某幾何體的三視圖如圖所示，則它的體積是(　　) A．8－ B．8－ C．8－2π D. 解析：圓錐的底面半徑為1，高為2，該幾何體體積為正方體體積減去圓錐體積，即V＝22×2－×π×12×2＝8－π，正確選項(xiàng)為A. 答案：A 4．(xx·山東)一空間幾何體的三視

3、圖如圖所示，則該幾何體的體積為(　　) A．2π＋2　　　　　　　　　　 B．4π＋2 C．2π＋ D．4π＋ 解析：由幾何體的三視圖可知，該幾何體是由一個底面直徑和高都是2的圓柱和一個底面邊長為，側(cè)棱長為2的正四棱錐疊放而成．故該幾何體的體積為 V＝π·12·2＋·()2·＝2π＋，故選C. 答案：C 5．[xx·四川卷] 某三棱錐的側(cè)視圖、俯視圖如圖1-1所示，則該三棱錐的體積是(錐體體積公式：V＝Sh，其中S為底面面積，h為高)(　　) 圖1-1 A．3 B．2 C. D．1 答案：D　[解析] 由圖可知，三棱錐的底面為邊長為2的正三角形，左側(cè)

4、面垂直于底面，且為邊長為2的正三角形，所以該三棱錐的底面積S＝×2×，高h(yuǎn)＝，所以其體積V＝Sh＝××＝1，故選D. 6.（xx山東，4分）如圖，正方體ABCD－A1B1C1D1的棱長為1，E、F分別為線段AA1，B1C上的點(diǎn)，則三棱錐D1－EDF的體積為________． 解析：因?yàn)镋點(diǎn)在線段AA1上，所以S△DED1＝×1×1＝，又因?yàn)镕點(diǎn)在線段B1C上，所以點(diǎn)F到平面DED1的距離為1，即h＝1，所以VD1－EDF＝VF－DED1＝×S△DED1×h＝××1＝. 答案： 7、(xx·遼寧高考)已知直三棱柱ABC－A1B1C1的6個頂點(diǎn)都在球O的球面上．若AB＝3，AC＝4，A

5、B⊥AC，AA1＝12，則球O的半徑為(　　) A. B．2 C. D．3 【解析】　因?yàn)橹比庵蠥B＝3，AC＝4，AA1＝12，AB⊥AC，所以BC＝5，且BC為過底面ABC的截面圓的直徑．取BC中點(diǎn)D，則OD⊥底面ABC，則O在側(cè)面BCC1B1內(nèi)，矩形BCC1B1的對角線長即為球直徑，所以2R＝＝13，即R＝. 8.[xx·山東卷] 一個六棱錐的體積為2，其底面是邊長為2的正六邊形，側(cè)棱長都相等，則該六棱錐的側(cè)面積為________． 答案 12　[解析] 設(shè)該六棱錐的高是h.根據(jù)體積公式得，V＝××2××6×h，解得h＝1，則側(cè)面三角形的高為＝2，所以側(cè)面積S＝×2

6、×2×6＝12. 9、[xx·浙江卷] 某幾何體的三視圖(單位：cm)如圖所示，則該幾何體的體積是( ) 圖1-1 A．72 cm3 B．90 cm3 C．108 cm3 D．138 cm3 答案B　[解析] 此幾何體是由長方體與三棱柱組合而成的，其體積為6×4×3＋×3×4×3＝90 cm3，故選B. 10、[xx·湖南卷] 一塊石材表示的幾何體的三視圖如圖1-2所示，將該石材切削、打磨，加工成球，則能得到的最大球的半徑等于(　　) 圖1-2 A．1 B．2 C．3 D．4 答案：B　[解析] 由三視圖可知，石材為一個三棱柱(相對應(yīng)的長方體的一半)，故可知能得到的最大球?yàn)槿庵膬?nèi)切球．由題意可知正視圖三角形的內(nèi)切圓的半徑即為球的半徑，可得R＝＝2.