《山東省濱州市2018屆高考數(shù)學(xué)一輪復(fù)習(xí) 課題四十一 排列組合二項式定理探究提升學(xué)案》由會員分享，可在線閱讀，更多相關(guān)《山東省濱州市2018屆高考數(shù)學(xué)一輪復(fù)習(xí) 課題四十一 排列組合二項式定理探究提升學(xué)案（2頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、 課題四十一 排列、組合、二項式定理 探究提升案 考綱要求 學(xué)習(xí)目標(biāo) 1.掌握分類計數(shù)原理與分步計數(shù)原理、并能用它分析和解決一些簡單的應(yīng)用問題．? 2．理解排列的意義，掌握排列數(shù)計算公式，并能用它解決一些簡單的應(yīng)用問題．? 3．理解組合的意義，掌握組合數(shù)計算公式和組合數(shù)性質(zhì)，并能用它們解決一些簡單的應(yīng)用問題．? 4．掌握二項式定理和二項展開式的性質(zhì)，并能用它們計算和證明一些簡單的問題．? 1.說出兩個計數(shù)原理和排列組合的概念，并會用計數(shù)原理推導(dǎo)排列數(shù)、組合數(shù)公式； 2.運(yùn)用二項式定理解決與二項展開式有關(guān)的簡單問題. 【使用說明及學(xué)法指導(dǎo)】1.先仔細(xì)閱讀教材選修2-3

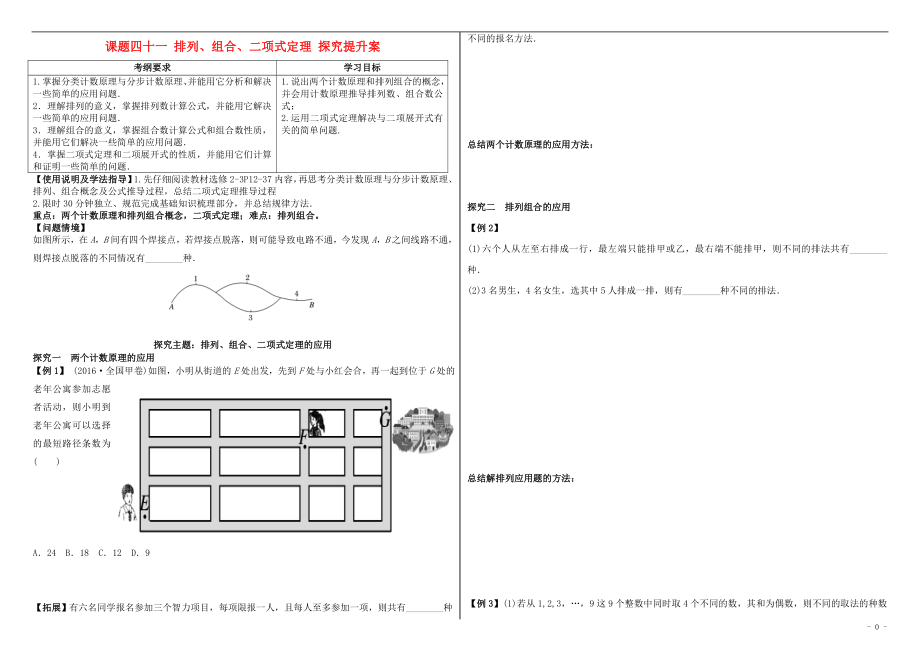
2、P12-37內(nèi)容，再思考分類計數(shù)原理與分步計數(shù)原理、排列、組合概念及公式推導(dǎo)過程，總結(jié)二項式定理推導(dǎo)過程 2.限時30分鐘獨立、規(guī)范完成基礎(chǔ)知識梳理部分，并總結(jié)規(guī)律方法． 重點：兩個計數(shù)原理和排列組合概念，二項式定理；難點：排列組合。 【問題情境】 如圖所示，在A，B間有四個焊接點，若焊接點脫落，則可能導(dǎo)致電路不通，今發(fā)現(xiàn)A，B之間線路不通，則焊接點脫落的不同情況有________種． 探究主題：排列、組合、二項式定理的應(yīng)用 探究一 兩個計數(shù)原理的應(yīng)用 【例1】 (2016·全國甲卷)如圖，小明從街道的E處出發(fā)，先到F處與小紅會合，再一起到位于G處的老年公寓參加志愿

3、者活動，則小明到老年公寓可以選擇的最短路徑條數(shù)為(　　) A．24 B．18 C．12 D．9 【拓展】有六名同學(xué)報名參加三個智力項目，每項限報一人，且每人至多參加一項，則共有________種不同的報名方法． 總結(jié)兩個計數(shù)原理的應(yīng)用方法： 探究二 排列組合的應(yīng)用 【例2】 (1)六個人從左至右排成一行，最左端只能排甲或乙，最右端不能排甲，則不同的排法共有________種． (2)3名男生，4名女生，選其中5人排成一排，則有________種不同的排法． 總結(jié)解排列應(yīng)用題的方法：

4、 【例3】(1)若從1,2,3，…，9這9個整數(shù)中同時取4個不同的數(shù)，其和為偶數(shù)，則不同的取法的種數(shù)是(　　) A．60 B．63 C．65 D．66 (2)要從12人中選出5人去參加一項活動，A，B，C三人必須入選，則有________種不同選法． 總結(jié)解組合應(yīng)用題的兩種類型： 探究三 二項式定理及其應(yīng)用 【例3】若展開式中前三項系數(shù)成等差數(shù)列.試求： （1）展開式中含x的一次項; （2）展開式中所有x的有理項； （3）二項式系數(shù)最大項. 【拓展】( ) A. B.85 C. D.274 【高考在線】 1. （2016年北京高考）在的展開式中，的系數(shù)為__________________.（用數(shù)字作答） 2.（2014山東）若的展開式中項的系數(shù)為20，則的最小值為 . 3.（2016年山東高考）若（ax2+）5的展開式中x5的系數(shù)是—80，則實數(shù)a=_______. 4.（2016年上海高考）在的二項式中，所有項的二項式系數(shù)之和為256，則常數(shù)項等于_________ - 1 -