《（浙江專用）2019高考數(shù)學(xué)二輪復(fù)習(xí) 指導(dǎo)二 透視高考解題模板示范規(guī)范拿高分 模板3 數(shù)列問題學(xué)案》由會員分享，可在線閱讀，更多相關(guān)《（浙江專用）2019高考數(shù)學(xué)二輪復(fù)習(xí) 指導(dǎo)二 透視高考解題模板示范規(guī)范拿高分 模板3 數(shù)列問題學(xué)案（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

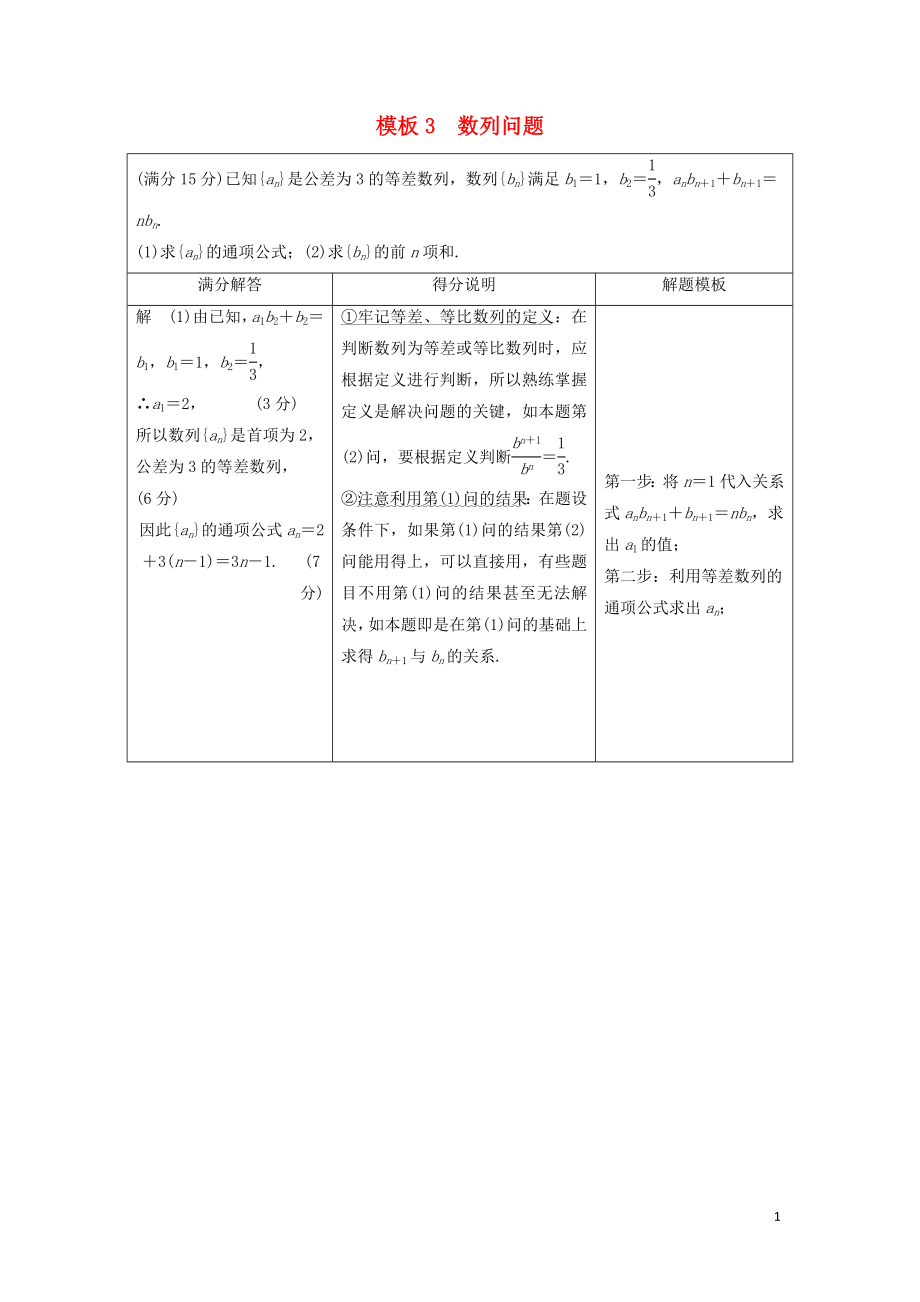
1、模板3　數(shù)列問題 (滿分15分)已知{an}是公差為3的等差數(shù)列，數(shù)列{bn}滿足b1＝1，b2＝，anbn＋1＋bn＋1＝nbn. (1)求{an}的通項(xiàng)公式；(2)求{bn}的前n項(xiàng)和. 滿分解答 得分說明 解題模板 解　(1)由已知，a1b2＋b2＝b1，b1＝1，b2＝， ∴a1＝2， (3分) 所以數(shù)列{an}是首項(xiàng)為2，公差為3的等差數(shù)列， (6分) 因此{(lán)an}的通項(xiàng)公式an＝2＋3(n－1)＝3n－1. (7分) ①牢記等差、等比數(shù)列的定義：在判斷數(shù)列為等差或等比數(shù)列時，應(yīng)根據(jù)定義進(jìn)行判斷，所以熟練掌握定義是解決問題的關(guān)鍵，

2、如本題第(2)問，要根據(jù)定義判斷＝. ②注意利用第(1)問的結(jié)果：在題設(shè)條件下，如果第(1)問的結(jié)果第(2)問能用得上，可以直接用，有些題目不用第(1)問的結(jié)果甚至無法解決，如本題即是在第(1)問的基礎(chǔ)上求得bn＋1與bn的關(guān)系. 第一步：將n＝1代入關(guān)系式anbn＋1＋bn＋1＝nbn，求出a1的值； 第二步：利用等差數(shù)列的通項(xiàng)公式求出an； 第三步：將第(1)問中求得的an代入關(guān)系式anbn＋1＋bn＋1＝nbn，求得bn＋1與bn的關(guān)系； 第四步：判斷數(shù)列{bn}為等比數(shù)列； 第五步：代入等比數(shù)列的前n項(xiàng)和公式求Sn. 第六步

3、：反思檢驗(yàn)，規(guī)范解題步驟. (2)由(1)和anbn＋1＋bn＋1＝nbn， 得bn＋1＝＝≠0，則＝， (11分) 因此數(shù)列{bn}是首項(xiàng)為1，公比為的等比數(shù)列， (12分) 設(shè)數(shù)列{bn}的前n項(xiàng)和為Sn，則 Sn＝＝－. (15分) ③寫全得分關(guān)鍵：寫清解題過程的關(guān)鍵點(diǎn)，有則給分，無則沒有分，同時解題過程中計算準(zhǔn)確，是得分的根本保證．如本題第(1)問要寫出a1b2＋b2＝b1，b1＝1，b2＝，才能得出a1，并指出數(shù)列{an}的性質(zhì)，否則不能得全分．第(2)問中一定要寫出求bn＋1＝的步驟并要指明{bn}的性質(zhì)；求Sn時，必須代入求和公式而不能直接寫出結(jié)

4、果，否則要扣分. 【訓(xùn)練3】 (2016·浙江卷)設(shè)數(shù)列{an}的前n項(xiàng)和為Sn，已知S2＝4，an＋1＝2Sn＋1，n∈N*. (1)求通項(xiàng)公式an； (2)求數(shù)列{|an－n－2|}的前n項(xiàng)和． 解　(1)由題意得則 又當(dāng)n≥2時，由an＋1－an＝(2Sn＋1)－(2Sn－1＋1)＝2an，得an＋1＝3an，同時a2＝3a1， ∴數(shù)列{an}的通項(xiàng)公式為an＝3n－1，n∈N*. (2)設(shè)bn＝|3n－1－n－2|，n∈N*，則b1＝2，b2＝1. 當(dāng)n≥3時，由于3n－1>n＋2， 故bn＝3n－1－n－2，n≥3. 設(shè)數(shù)列{bn}的前n項(xiàng)和為Tn， 則T1＝2，T2＝3， 當(dāng)n≥3時，Tn＝3＋－＝，此時T2符合，T1不符合， ∴Tn＝ 3