《2022年高中數(shù)學(xué) 第六教時(shí) 函數(shù)圖象教案 新人教A版必修1》由會(huì)員分享，可在線閱讀，更多相關(guān)《2022年高中數(shù)學(xué) 第六教時(shí) 函數(shù)圖象教案 新人教A版必修1（2頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

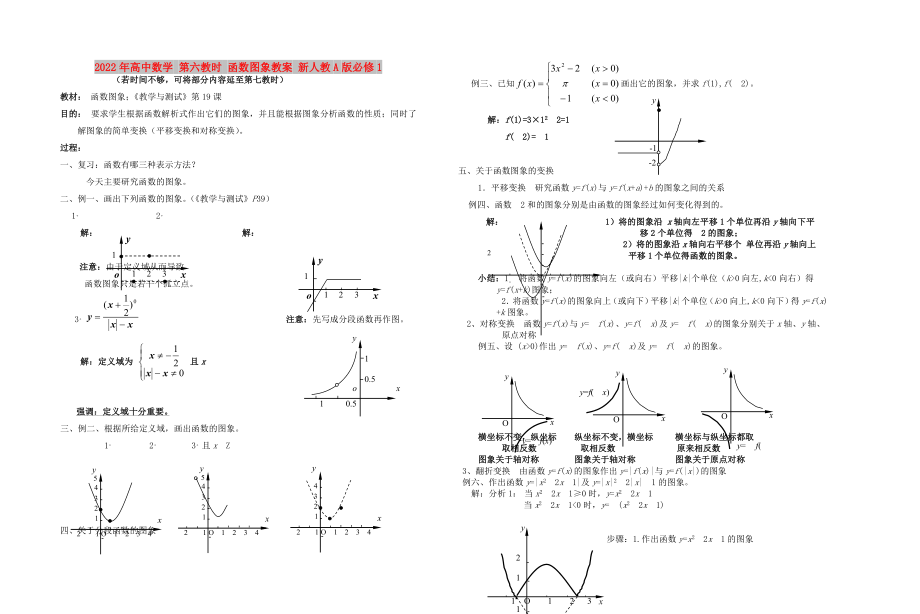
1、2022年高中數(shù)學(xué) 第六教時(shí) 函數(shù)圖象教案 新人教A版必修1 （若時(shí)間不夠，可將部分內(nèi)容延至第七教時(shí)） 教材： 函數(shù)圖象；《教學(xué)與測(cè)試》第19課 目的： 要求學(xué)生根據(jù)函數(shù)解析式作出它們的圖象，并且能根據(jù)圖象分析函數(shù)的性質(zhì)；同時(shí)了解圖象的簡(jiǎn)單變換（平移變換和對(duì)稱變換）。 過(guò)程： 一、復(fù)習(xí)：函數(shù)有哪三種表示方法？ 今天主要研究函數(shù)的圖象。 二、例一、畫出下列函數(shù)的圖象。（《教學(xué)與測(cè)試》P39） o x y 1 2 3 -1 1 1。 2。 解：

2、 解： o x y 1 2 3 -1 1 注意：由于定義域從而導(dǎo)致 函數(shù)圖象只是若干個(gè)孤立點(diǎn)。 -1 -0.5 1 0.5 y o x 3。 注意：先寫成分段函數(shù)再作圖。 解：定義域?yàn)? 且x1 強(qiáng)調(diào)：定義域十分重要。 三、例二、根據(jù)所給定義域，畫出函數(shù)的圖象。 -2 -1 O 1 2 3 4 y

3、 x 1 2 3 4 -2 -1 O 1 2 3 4 y x 1 2 3 4 -2 -1 O 1 2 3 4 y x 1 2 3 4 5 5 1。 2。 3。且x?Z 四、關(guān)于分段函數(shù)的圖象 -1 -2 p y 例三、已知 畫出它的圖象，并求f(1),f(-2)。 解：f(1)=3×12-2=1

4、 f(-2)=-1 五、關(guān)于函數(shù)圖象的變換 1．平移變換 研究函數(shù)y=f(x)與y=f(x+a)+b的圖象之間的關(guān)系 例四、函數(shù)-2和的圖象分別是由函數(shù)的圖象經(jīng)過(guò)如何變化得到的。 解： 1）將的圖象沿 x軸向左平移1個(gè)單位再沿y軸向下平移2個(gè)單位得-2的圖象； -2 2）將的圖象沿x軸向右平移個(gè) 單位再沿y軸向上平移1個(gè)單位得函數(shù)的圖象。 小結(jié)：1。 將函數(shù)y=f(x)的圖象向左（或向右）平移|k|個(gè)單位（k>0向左,k<0向右）得y=f(x+k)圖象； 2．將函數(shù)y=f(x)的圖

5、象向上（或向下）平移|k|個(gè)單位（k>0向上,k<0向下）得y=f(x) +k圖象。 2、對(duì)稱變換 函數(shù)y=f(x)與y=-f(x)、y=f(-x)及y=-f(-x)的圖象分別關(guān)于x軸、y軸、原點(diǎn)對(duì)稱 y x O y x O y x O y=-f(x) y=f(-x) y=-f(-x) 例五、設(shè) (x>0)作出y=-f(x)、y=f(-x)及y=-f(-x)的圖象。 橫坐標(biāo)不變，縱坐標(biāo) 縱坐標(biāo)不變，橫坐標(biāo) 橫坐標(biāo)與縱坐標(biāo)都取 取相反數(shù) 取相反數(shù) 原來(lái)相反數(shù) 圖象關(guān)于軸對(duì)

6、稱 圖象關(guān)于軸對(duì)稱 圖象關(guān)于原點(diǎn)對(duì)稱 3、翻折變換 由函數(shù)y=f(x)的圖象作出y=|f(x)|與y=f(|x|)的圖象 例六、作出函數(shù)y=|x2-2x-1|及y=|x|2-2|x|-1的圖象。 解：分析1： 當(dāng)x2-2x-1≥0時(shí)，y=x2-2x-1 當(dāng)x2-2x-1<0時(shí)，y=-(x2-2x-1) y x -1 O 1 2 3 2 1 -1 -2 步驟：1.作出函數(shù)y=x2-2x-1的圖象

7、 2．將上述圖象x軸下方部分以x軸為對(duì)稱軸向上翻折（上方部分不變），即得y=|x2-2x-1|的圖象。 分析2：當(dāng)x≥0時(shí) y=x2-2x-1 當(dāng)x<0時(shí) y=x2+2x-1 即 y=(-x)2-2(-x)-1 y x -3 -2 -1 O 1 2 3 3 2 1 -1 -2 -3 步驟：1）作出y=x2-2x-1的圖象； 2）y軸右方部分不變，再將右方部分以y軸為對(duì)稱軸向左翻折，即得y=|x|2-2|x|-1的圖象 。 小結(jié)： 將y=f(x)的圖象，x軸上方部分不變，下方部分以x軸為對(duì)稱軸向上翻折即得y=|f(x)|的圖象； 將y=f(x)的圖象，y軸右方部分不變，以y軸為對(duì)稱軸將右方部分向左翻折即得y=f(|x|)的圖象。 六、作業(yè)： 《教學(xué)與測(cè)試》 P40 7、8 《課課練》 P53 3 P54 9 《精編》 P83 24、25、26 （第26題應(yīng)作啟發(fā)： ）