《2013高考數(shù)學(xué) 考前知識(shí)要點(diǎn)復(fù)習(xí)三 數(shù)列》由會(huì)員分享，可在線閱讀，更多相關(guān)《2013高考數(shù)學(xué) 考前知識(shí)要點(diǎn)復(fù)習(xí)三 數(shù)列（6頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

1、高中數(shù)學(xué) 第三章 數(shù)列 考試內(nèi)容： 數(shù)列． 等差數(shù)列及其通項(xiàng)公式．等差數(shù)列前n項(xiàng)和公式． 等比數(shù)列及其通項(xiàng)公式．等比數(shù)列前n項(xiàng)和公式． 考試要求： （1）理解數(shù)列的概念，了解數(shù)列通項(xiàng)公式的意義了解遞推公式是給出數(shù)列的一種方法，并能根據(jù)遞推公式寫出數(shù)列的前幾項(xiàng)． （2）理解等差數(shù)列的概念，掌握等差數(shù)列的通項(xiàng)公式與前n項(xiàng)和公式，并能解決簡(jiǎn)單的實(shí)際問題． （3）理解等比數(shù)列的概念，掌握等比數(shù)列的通項(xiàng)公式與前n項(xiàng)和公式，井能解決簡(jiǎn)單的實(shí)際問題． §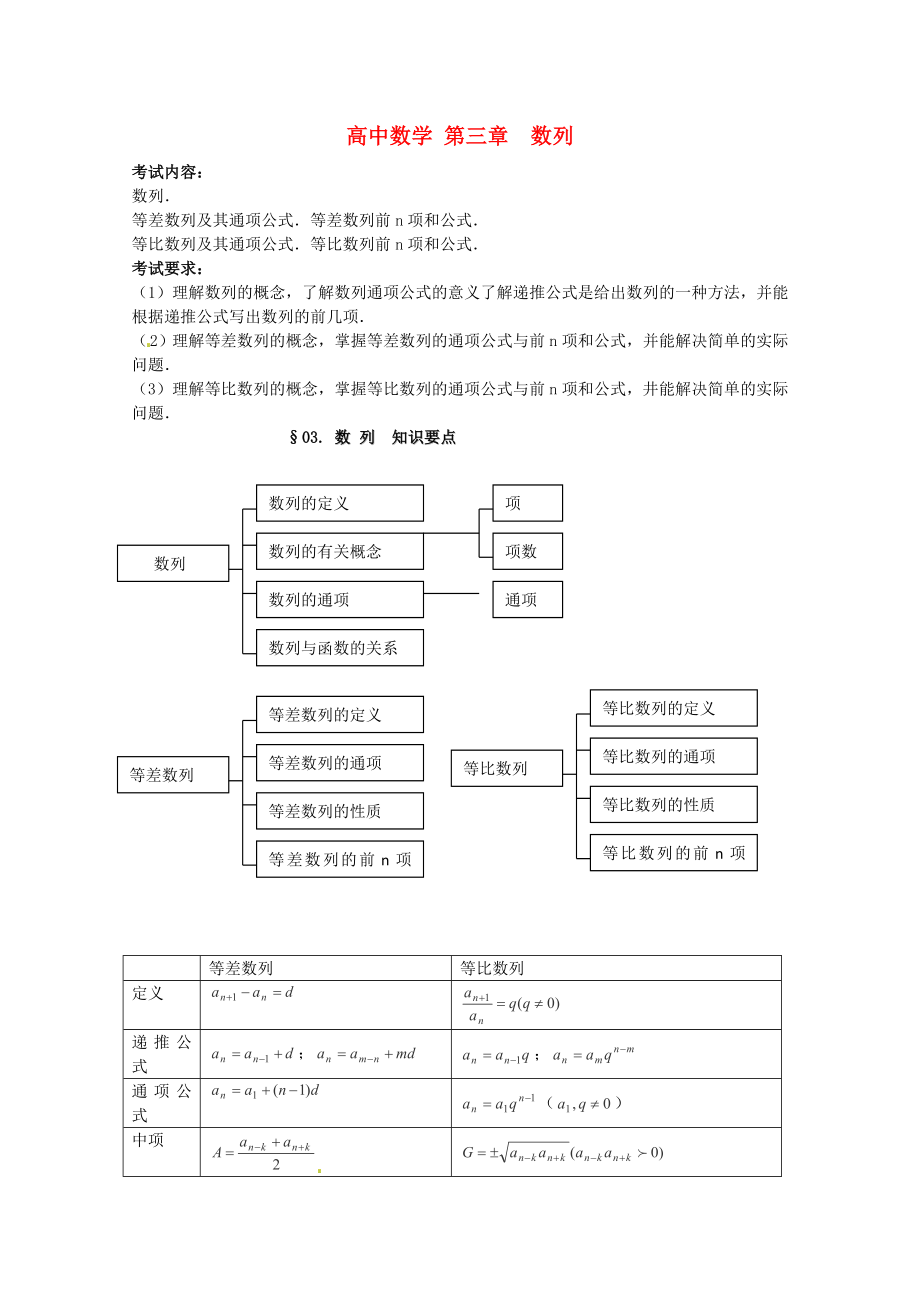03. 數(shù) 列 知識(shí)要點(diǎn) 數(shù)列 數(shù)列的定義 數(shù)列的有關(guān)概念 數(shù)列的通項(xiàng) 數(shù)列與

2、函數(shù)的關(guān)系 項(xiàng) 項(xiàng)數(shù) 通項(xiàng) 等差數(shù)列 等差數(shù)列的定義 等差數(shù)列的通項(xiàng) 等差數(shù)列的性質(zhì) 等差數(shù)列的前n項(xiàng)和 等比數(shù)列 等比數(shù)列的定義 等比數(shù)列的通項(xiàng) 等比數(shù)列的性質(zhì) 等比數(shù)列的前n項(xiàng)和 等差數(shù)列 等比數(shù)列 定義 遞推公式 ； ； 通項(xiàng)公式 （） 中項(xiàng) （） （） 前項(xiàng)和 重要性質(zhì) 1. ⑴等差、等比數(shù)列： 等差數(shù)列 等比數(shù)列 定義 通項(xiàng)公式 =+（n-1）d=+（n-k）d=+-d 求

3、和公式 中項(xiàng)公式 A= 推廣：2= 。推廣： 性質(zhì) 1 若m+n=p+q則 若m+n=p+q，則。 2 若成A.P（其中）則也為A.P。 若成等比數(shù)列 （其中），則成等比數(shù)列。 3 ． 成等差數(shù)列。 成等比數(shù)列。 4 ， 5 ⑵看數(shù)列是不是等差數(shù)列有以下三種方法： ① ②2() ③(為常數(shù)). ⑶看數(shù)列是不是等比數(shù)列有以下四種方法： ① ②(，)① 注①：i. ，是a、b、c成等比的雙非條件，即a、b、c等比數(shù)列. ii. （ac＞0）→為a、b、c等比數(shù)列的充分不必要. iii. →為a、b、c

4、等比數(shù)列的必要不充分. iv. 且→為a、b、c等比數(shù)列的充要. 注意：任意兩數(shù)a、c不一定有等比中項(xiàng)，除非有ac＞0，則等比中項(xiàng)一定有兩個(gè). ③(為非零常數(shù)). ④正數(shù)列{}成等比的充要條件是數(shù)列{}（）成等比數(shù)列. ⑷數(shù)列{}的前項(xiàng)和與通項(xiàng)的關(guān)系： [注]： ①（可為零也可不為零→為等差數(shù)列充要條件（即常數(shù)列也是等差數(shù)列）→若不為0，則是等差數(shù)列充分條件）. ②等差{}前n項(xiàng)和 →可以為零也可不為零→為等差的充要條件→若為零，則是等差數(shù)列的充分條件；若不為零，則是等差數(shù)列的充分條件. ③非零常數(shù)列既可為等比數(shù)列，也可為等差數(shù)列.（不是非零，即不可能有等比數(shù)列） 2.

5、 ①等差數(shù)列依次每k項(xiàng)的和仍成等差數(shù)列，其公差為原公差的k2倍； ②若等差數(shù)列的項(xiàng)數(shù)為2，則； ③若等差數(shù)列的項(xiàng)數(shù)為，則，且， . 3. 常用公式：①1+2+3 …+n = ② ③ [注]：熟悉常用通項(xiàng)：9，99，999，…； 5，55，555，…. 4. 等比數(shù)列的前項(xiàng)和公式的常見應(yīng)用題： ⑴生產(chǎn)部門中有增長率的總產(chǎn)量問題. 例如，第一年產(chǎn)量為，年增長率為，則每年的產(chǎn)量成等比數(shù)列，公比為. 其中第年產(chǎn)量為，且過年后總產(chǎn)量為： ⑵銀行部門中按復(fù)利計(jì)算問題. 例如：一年中每月初到銀行存元，利息為，每月利息按復(fù)利計(jì)算，則每月的元過個(gè)月后便成為元

6、. 因此，第二年年初可存款： =. ⑶分期付款應(yīng)用題：為分期付款方式貸款為a元；m為m個(gè)月將款全部付清；為年利率. 5. 數(shù)列常見的幾種形式： ⑴（p、q為二階常數(shù)）用特證根方法求解. 具體步驟：①寫出特征方程（對(duì)應(yīng)，x對(duì)應(yīng)），并設(shè)二根②若可設(shè)，若可設(shè)；③由初始值確定. ⑵（P、r為常數(shù)）用①轉(zhuǎn)化等差，等比數(shù)列；②逐項(xiàng)選代；③消去常數(shù)n轉(zhuǎn)化為的形式，再用特征根方法求；④（公式法），由確定. ①轉(zhuǎn)化等差，等比：. ②選代法： . ③用特征方程求解：. ④由選代法推導(dǎo)結(jié)果：. 6. 幾種常見的數(shù)列的思想方法： ⑴等差數(shù)列的前項(xiàng)和為，在時(shí)，有最大值. 如何確定使取最大值

7、時(shí)的值，有兩種方法： 一是求使，成立的值；二是由利用二次函數(shù)的性質(zhì)求的值. ⑵如果數(shù)列可以看作是一個(gè)等差數(shù)列與一個(gè)等比數(shù)列的對(duì)應(yīng)項(xiàng)乘積，求此數(shù)列前項(xiàng)和可依照等比數(shù)列前項(xiàng)和的推倒導(dǎo)方法：錯(cuò)位相減求和. 例如： ⑶兩個(gè)等差數(shù)列的相同項(xiàng)亦組成一個(gè)新的等差數(shù)列，此等差數(shù)列的首項(xiàng)就是原兩個(gè)數(shù)列的第一個(gè)相同項(xiàng)，公差是兩個(gè)數(shù)列公差的最小公倍數(shù). 2. 判斷和證明數(shù)列是等差（等比）數(shù)列常有三種方法：(1)定義法:對(duì)于n≥2的任意自然數(shù),驗(yàn)證為同一常數(shù)。(2)通項(xiàng)公式法。(3)中項(xiàng)公式法:驗(yàn)證都成立。 3. 在等差數(shù)列｛｝中,有關(guān)Sn 的最值問題：(1)當(dāng)>0,d<0時(shí)，滿足的項(xiàng)數(shù)m使得取最大

8、值. (2)當(dāng)<0,d>0時(shí)，滿足的項(xiàng)數(shù)m使得取最小值。在解含絕對(duì)值的數(shù)列最值問題時(shí),注意轉(zhuǎn)化思想的應(yīng)用。 （三）、數(shù)列求和的常用方法 1. 公式法:適用于等差、等比數(shù)列或可轉(zhuǎn)化為等差、等比數(shù)列的數(shù)列。 2.裂項(xiàng)相消法:適用于其中{ }是各項(xiàng)不為0的等差數(shù)列，c為常數(shù)；部分無理數(shù)列、含階乘的數(shù)列等。 　　　3.錯(cuò)位相減法:適用于其中{ }是等差數(shù)列，是各項(xiàng)不為0的等比數(shù)列。 4.倒序相加法: 類似于等差數(shù)列前n項(xiàng)和公式的推導(dǎo)方法. 5.常用結(jié)論 1）: 1+2+3+...+n = 2） 1+3+5+...+(2n-1) = 3） 4） 5） 6）