《高中數(shù)學(xué)學(xué)考復(fù)習(xí) 模塊過關(guān)專題講座練習(xí) 第五講直線與平面平行的判定與性質(zhì) 新人教A版必修2》由會(huì)員分享，可在線閱讀，更多相關(guān)《高中數(shù)學(xué)學(xué)考復(fù)習(xí) 模塊過關(guān)專題講座練習(xí) 第五講直線與平面平行的判定與性質(zhì) 新人教A版必修2（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

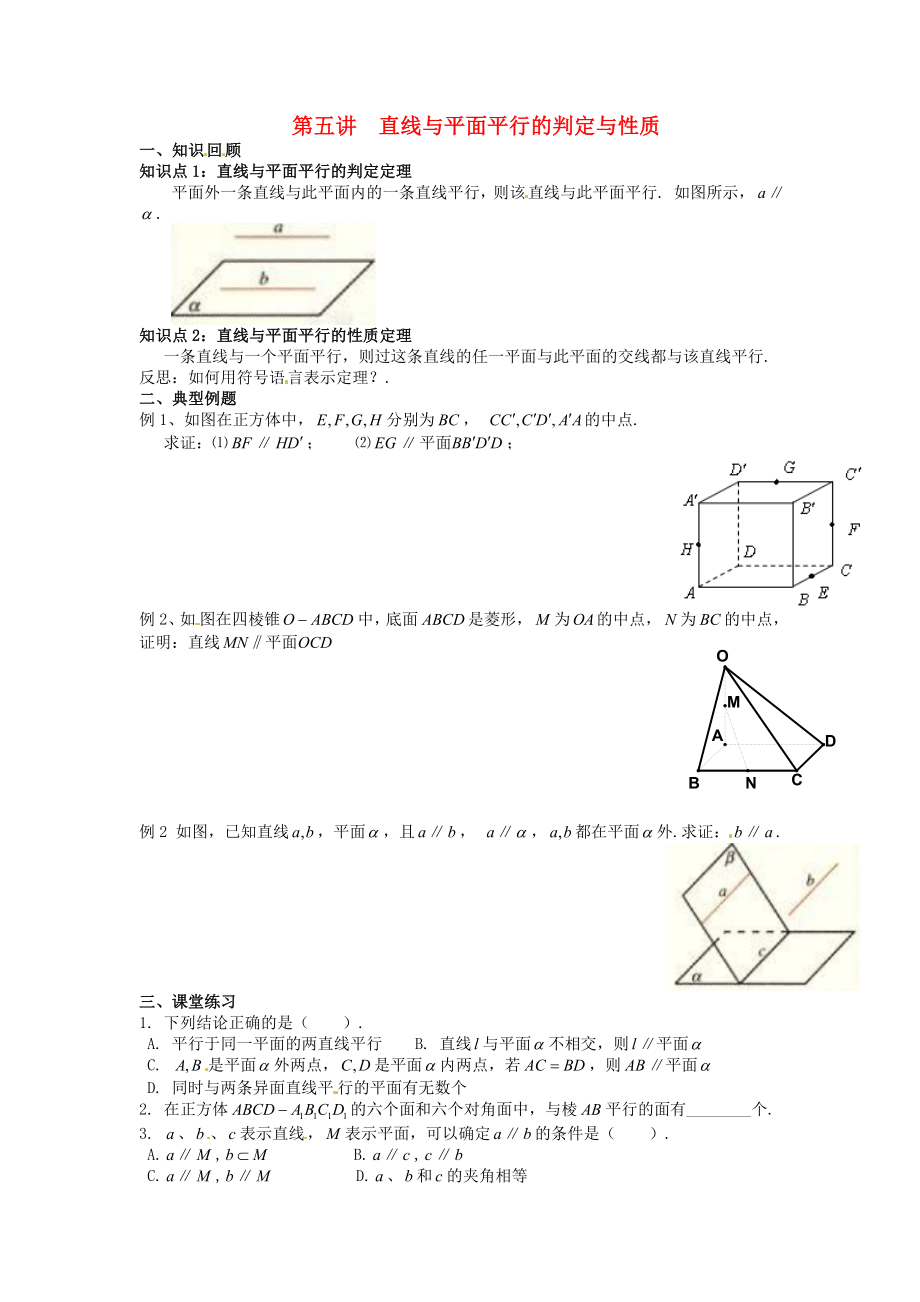
1、第五講 直線與平面平行的判定與性質(zhì) 一、知識(shí)回顧 知識(shí)點(diǎn)1：直線與平面平行的判定定理 平面外一條直線與此平面內(nèi)的一條直線平行，則該直線與此平面平行. 如圖所示，∥. 知識(shí)點(diǎn)2：直線與平面平行的性質(zhì)定理 一條直線與一個(gè)平面平行，則過這條直線的任一平面與此平面的交線都與該直線平行. 反思：如何用符號(hào)語(yǔ)言表示定理？. 二、典型例題 例1、如圖在正方體中，分別為， 的中點(diǎn). 求證：⑴∥； ⑵∥； 例2、如圖在四棱錐中，底面是菱形，為的中點(diǎn)，為的中點(diǎn)， 證明：直線 例2 如圖，已知直線，平面，且∥， ∥，都在平

2、面外.求證：∥. 三、課堂練習(xí) 1. 下列結(jié)論正確的是（ ）. A. 平行于同一平面的兩直線平行 B. 直線與平面不相交，則∥平面 C. 是平面外兩點(diǎn)，是平面內(nèi)兩點(diǎn)，若，則∥平面 D. 同時(shí)與兩條異面直線平行的平面有無(wú)數(shù)個(gè) 2. 在正方體的六個(gè)面和六個(gè)對(duì)角面中，與棱平行的面有________個(gè). 3. 、、表示直線，表示平面，可以確定∥的條件是（ ）. A.∥, B.∥,∥ C.∥,∥ D.、和的夾角相等 4. 和是異面直線，則經(jīng)過可作___個(gè)平面與直線平行. 5. 如圖，在正三棱柱中，是的中點(diǎn)，求證：∥

3、面. 四、總結(jié)提升 1. 直線與平面平行的判定定理及其應(yīng)用，其核心是線線平行線面平行； 2. 直線和平面平行的性質(zhì)定理及其運(yùn)用，其核心是線面平行線線平行 ※ 知識(shí)拓展 1．判定直線與平面平行通常有三種方法： ⑴利用定義：證明直線與平面沒有公共點(diǎn).但直接證明是困難的，往往借助于反正法來證明. ⑵利用判定定理，其關(guān)鍵是證明線線平行.證明線線平行可利用平行公理、中位線、比例線段等等. ⑶利用平面與平面平行的性質(zhì).(后面將會(huì)學(xué)習(xí)到) 2．在證明線線或線面平行的時(shí)候，直線和平面平行的判定定理和性質(zhì)定理在解題時(shí)往往交替使用，相互轉(zhuǎn)換，即線面平行問題往往轉(zhuǎn)化為線線平行問題，線線平行問題又轉(zhuǎn)化為線面平行問題，反復(fù)運(yùn)用，直到得出結(jié)論. 3．反證法：先提出和原命題中的結(jié)論相反的假定，然后從這個(gè)假定中得出和已知條件相矛盾的結(jié)果，這樣就否定了原來的假定而肯定原命題. 4．同一法：欲證圖形有某種特性時(shí)，可另作一個(gè)具有同樣特征的圖形，再證明所作圖形和已知條件中的圖形是同一個(gè).如果不是同一個(gè)，則與某公理或定理相矛盾. 五、課后作業(yè) 1. 如圖，四邊形是矩形，是、的中點(diǎn)，求證：∥面. 2. 如圖所示，已知∥，，， ，求證：∥∥. 3.形與矩形交于，和分別為和的中點(diǎn)，.求證：∥平面.