《江蘇省南通市高三下學(xué)期第二次調(diào)研測試 數(shù)學(xué)試題及答案》由會員分享，可在線閱讀，更多相關(guān)《江蘇省南通市高三下學(xué)期第二次調(diào)研測試 數(shù)學(xué)試題及答案（19頁珍藏版）》請在裝配圖網(wǎng)上搜索。

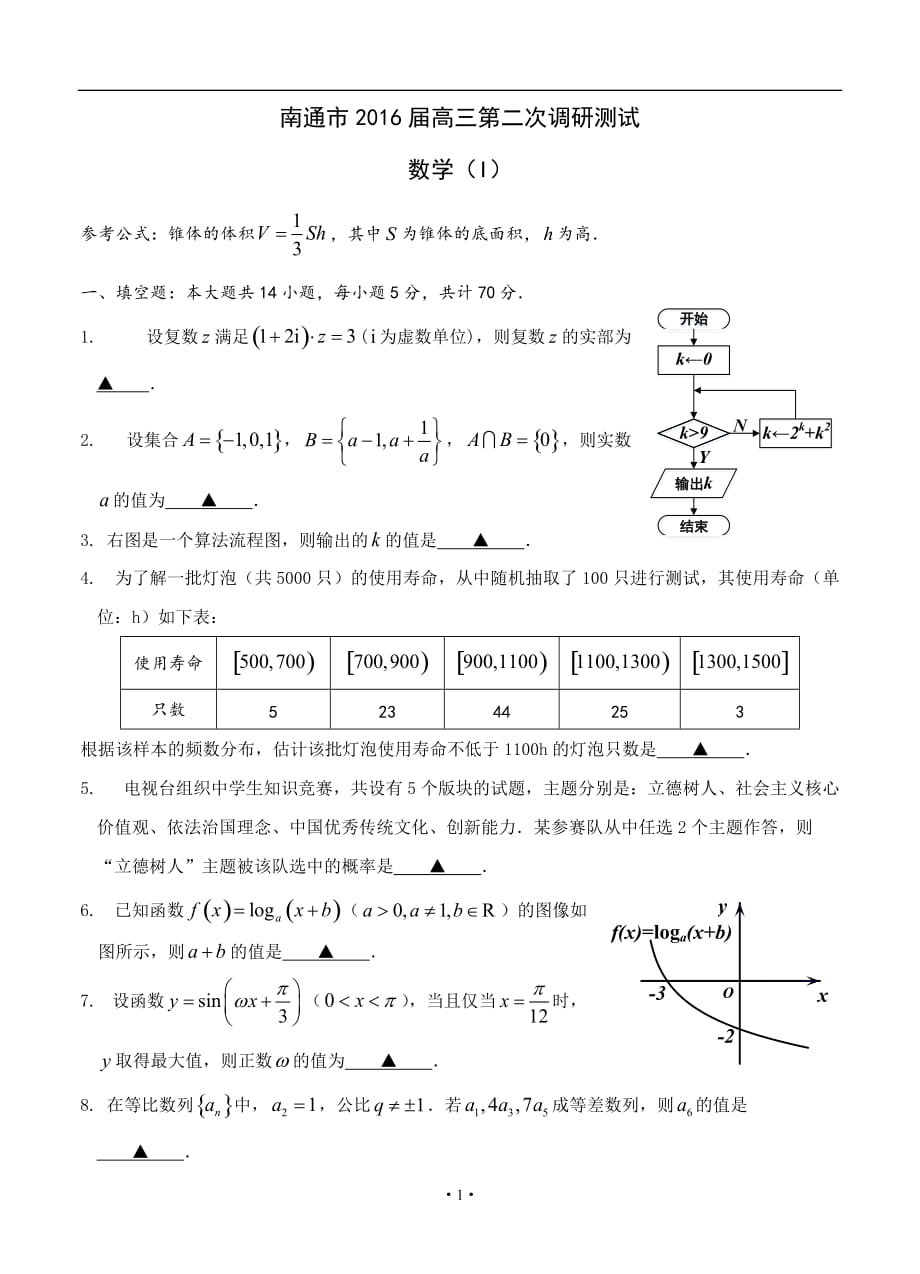
1、 南通市2016屆高三第二次調(diào)研測試 數(shù)學(xué)（I） 參考公式：錐體的體積，其中為錐體的底面積，為高． 一、填空題：本大題共14小題，每小題5分，共計70分． 1. 設(shè)復(fù)數(shù)滿足(為虛數(shù)單位)，則復(fù)數(shù)的實部為 ▲ ． 2. 設(shè)集合，，，則實數(shù)的值為 ▲ ． 3. 右圖是一個算法流程圖，則輸出的的值是 ▲ ． 4. 為了解一批燈泡（共5000只）的使用壽命，從中隨機抽取了100只進(jìn)行測試，其使用壽命（單位：h）如下表： 使用壽命 只數(shù) 5 23 44 25 3 根據(jù)該樣本的頻數(shù)分布，估計該批燈泡使用壽命不低于110

2、0h的燈泡只數(shù)是 ▲ ． 5. 電視臺組織中學(xué)生知識競賽，共設(shè)有5個版塊的試題，主題分別是：立德樹人、社會主義核心價值觀、依法治國理念、中國優(yōu)秀傳統(tǒng)文化、創(chuàng)新能力．某參賽隊從中任選2個主題作答，則“立德樹人”主題被該隊選中的概率是 ▲ ． 6. 已知函數(shù)（）的圖像如圖所示，則的值是 ▲ ． 7. 設(shè)函數(shù)（），當(dāng)且僅當(dāng)時，取得最大值，則正數(shù)的值為 ▲ ． 8. 在等比數(shù)列中，，公比．若成等差數(shù)列，則的值是 ▲ ． 9. 在體積為的四面體中，平面，，，，則長度的所有值為 ▲ ． 10. 在平面直角坐標(biāo)系中，過點

3、的直線與圓相切于點，與圓相交于點，且，則正數(shù)的值為 ▲ ． 11. 已知是定義在上的偶函數(shù)，且對于任意的，滿足，若當(dāng)時，，則函數(shù)在區(qū)間上的零點個數(shù)為 ▲ ． 12. 如圖，在同一平面內(nèi)，點位于兩平行直線的同側(cè)，且到的距離分別為1，3．點分別在，，則的最大值是 ▲ ． 13. 設(shè)實數(shù)滿足，則的最小值是 ▲ ． 14. 若存在，使得，則實數(shù)的取值范圍是 ▲ ． 二、解答題：本大題共6小題，共計90分． 15. 在斜三角形中，． （1）求的值； （2）若，，求的周長． 16. 如圖，在正方體中，分別為棱的中點．

4、求證：（1）平面； （2）平面平面． 17. 植物園擬建一個多邊形苗圃，苗圃的一邊緊靠著長度大于30m的圍墻．現(xiàn)有兩種方案： 方案① 多邊形為直角三角形（），如圖1所示，其中； 方案② 多邊形為等腰梯形（），如圖2所示，其中． 請你分別求出兩種方案中苗圃的最大面積，并從中確定使苗圃面積最大的方案． 18. 如圖，在平面直角坐標(biāo)系中，已知橢圓（）的離心率為．為橢圓上異于頂點的一點，點滿足． （1）若點的坐標(biāo)為，求橢圓的方程； （2）設(shè)過點的一條直線交橢圓于兩點，且，直線的斜率之積為，求實數(shù)的值． 19. 設(shè)函數(shù)，，其中是實數(shù)． （1）若，解不

5、等式； （2）若，求關(guān)于的方程實根的個數(shù)． 20. 設(shè)數(shù)列的各項均為正數(shù)，的前項和，． （1）求證：數(shù)列為等差數(shù)列； （2）等比數(shù)列的各項均為正數(shù)，，，且存在整數(shù)，使得． （i）求數(shù)列公比的最小值（用表示）； （ii）當(dāng)時，，求數(shù)列的通項公式． 數(shù)學(xué)（II）（附加題） 21（B）．在平面直角坐標(biāo)系中，設(shè)點在矩陣對應(yīng)的變換作用下得到點，將點繞點逆時針旋轉(zhuǎn)得到點，求點的坐標(biāo)． 21（C）．在平面直角坐標(biāo)系中，已知直線（為參數(shù)）與曲線 （為參數(shù)）相交于兩點，求線段的長． 22．一個摸球游戲，規(guī)則如下：在一不透明的紙盒中，裝有6個大小相同、顏色各異的玻璃球．參加者交費

6、1元可玩1次游戲，從中有放回地摸球3次．參加者預(yù)先指定盒中的某一種顏色的玻璃球，然后摸球．當(dāng)所指定的玻璃球不出現(xiàn)時，游戲費被沒收；當(dāng)所指定的玻璃球出現(xiàn)1次，2次，3次時，參加者可相應(yīng)獲得游戲費的0倍，1倍，倍的獎勵（），且游戲費仍退還給參加者．記參加者玩1次游戲的收益為元． （1）求概率的值； （2）為使收益的數(shù)學(xué)期望不小于0元，求的最小值． （注：概率學(xué)源于賭博，請自覺遠(yuǎn)離不正當(dāng)?shù)挠螒颍。? 23．設(shè)（），其中（）．當(dāng)除以4的余數(shù)是（）時，數(shù)列的個數(shù)記為． （1）當(dāng)時，求的值； （2）求關(guān)于的表達(dá)式，并化簡． 19