《九年級數(shù)學(xué)上冊第一章你能證明它們嗎導(dǎo)學(xué)案1無答案北師大版》由會員分享��,可在線閱讀�,更多相關(guān)《九年級數(shù)學(xué)上冊第一章你能證明它們嗎導(dǎo)學(xué)案1無答案北師大版(4頁珍藏版)》請在裝配圖網(wǎng)上搜索�����。
1、甘肅省張掖市臨澤縣第二中學(xué)九年級數(shù)學(xué)上冊 第一章《你能證明它們嗎�����?》導(dǎo)學(xué)案(1)(無答案) 北師大版
課題
課型
新授課
課時
1
教師
教學(xué)目標
1����、了解作為證明基礎(chǔ)的幾條公理的內(nèi)容�,掌握證明的基本步驟和書寫格式�。
2����、經(jīng)歷“探索-發(fā)現(xiàn)-猜想-證明”的過程。能夠用綜合法證明等腰三角形的關(guān)性質(zhì)定理���。
重點
了解所學(xué)公理的內(nèi)容,通過等腰三角形性質(zhì)證明���,掌握證明的基本步驟和書寫格式���。
難點
證明等腰三角形性質(zhì)時輔助線做法���。
教法
合作探究
學(xué)法
合作交流
時間
一�、 初生牛犢不怕虎,讓我來探索:
1�、 前置準備:請你用自己的語言說一說證明的基本步
2�、驟�。
2�����、 列舉我們已知道的公理:���、
(1)公理:同位角 ,兩直線平行�����。
(2)公理:兩直線 ��,同位角 �。
(3)公理: 的兩個三角形全等。(簡稱 �����,字母表示 )
(4)公理: 的兩個三角形全等。 (簡稱 �����,字母表示 )
(5)公理: 的兩個三角形全等�����。(簡稱 ��,字母
3��、表示 )
(6)公理:全等三角形的對應(yīng)邊 ��,對應(yīng)角 �。
注:等式的有關(guān)性質(zhì)和不等式的有關(guān)性質(zhì)都可以看作公理。
你能解決這個問題么����?
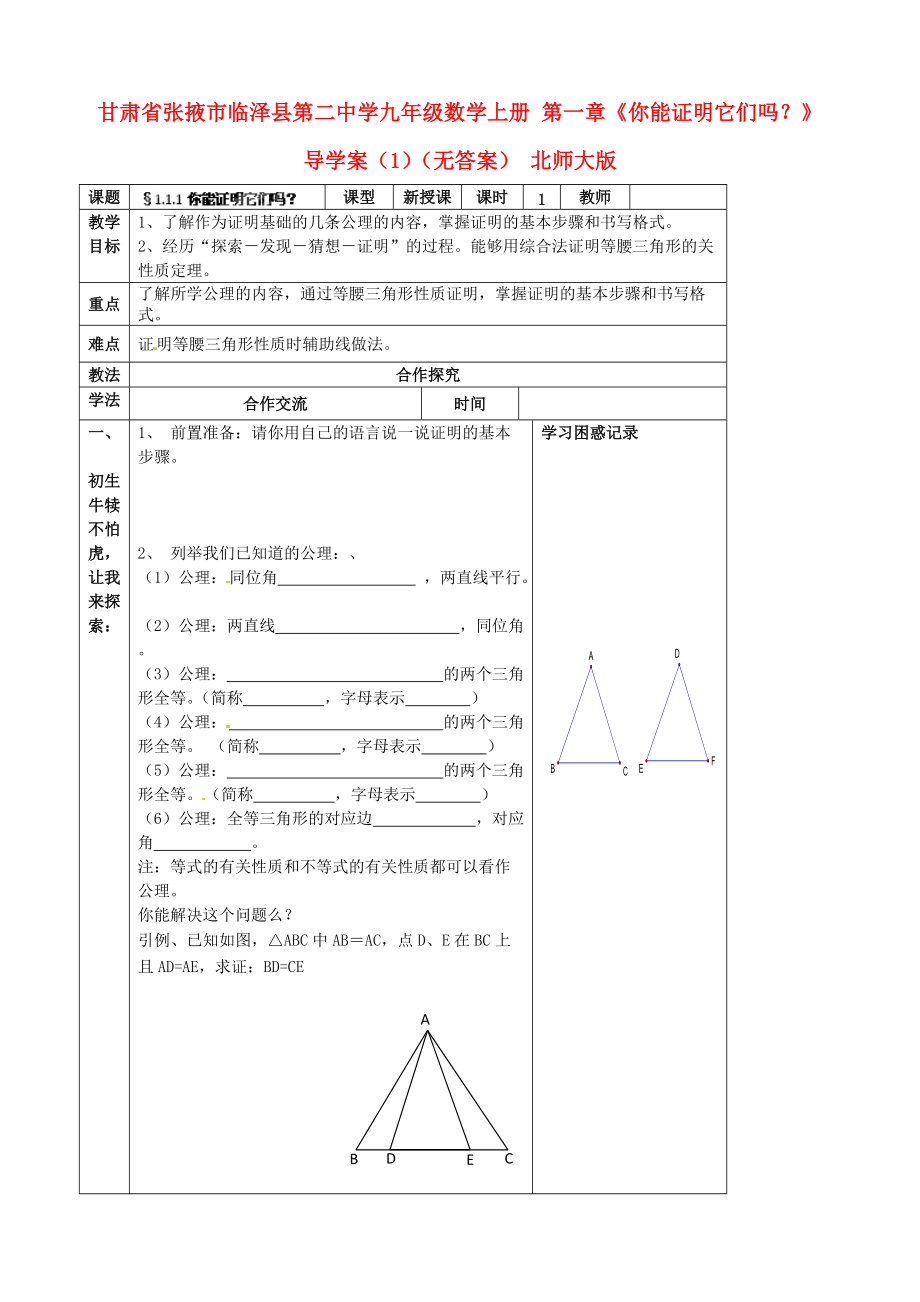
引例、已知如圖,△ABC中AB=AC����,點D�、E在BC上且AD=AE,求證:BD=CE
A
B
D
E
C
學(xué)習(xí)困惑記錄
二��、講授新課
探索一:三角形全等的判定
1�、 判定一般的三角形全等還有一種方法是什么?
推論: (簡寫為
4���、 )
你能證明嗎�?
已知:在△ABC和△DEF中�����,∠A=∠D,∠B=∠E,BC=EF���,求證:△ABC≌△DEF
索二:等腰三角形的性質(zhì)定理
1��、等腰三角形性質(zhì):等腰三角形的兩個 相等(簡稱:等 對等 )
已知:如圖�,在△ABC中�����,AB=AC,求證:∠B=∠C
證明一:取BC的中點D���,連接AD
2����、推論:等腰三角形的頂角的 ���、底邊上的 �、底邊上的 互相重合(簡稱: )
3���、請證明:推論2:等邊三角形的三個角都是
5����、 ��,并且每個角都等于 �。
二、我的課堂我做主
1���、在△ABC和△DEF中��,以下四個命題中假命題是【 】
A����、由AB=DE,BC=EF�,∠B=∠E��,可判斷△ABC≌△DEF�;
B、由∠A=∠D�,∠C=∠F,AC=DF�����,可判斷△ABC≌△DEF��;
C���、由AB=DE��,AC=DF����,BC=EF,可判斷△ABC≌△DEF�����;
D���、由∠A=∠D��,∠B=∠E�,AC=EF�����,可判斷△ABC≌△DEF��。
2����、下列各組幾何圖形中,一定全等的是( )
A���、各有一個角是550的兩個等腰三角形����;B、兩個等邊三角形�����;
6����、
C、腰長相等的兩個等腰直角三角形��;D�����、各有一個角是500���,腰長都為6cm的兩個等腰三角形.
3、如圖���,已知:∥��,AB=CD�,若要使△ABE≌△CDF,仍需添加一個條件��,
下列條件中,哪一個不能使△ABE≌△CDF的是( )
A�、∠A=∠B ; B、BF=CE; C���、AE∥DF; D�、AE=DF.
4��、若等腰三角形中有一個角等于50����,則等腰三角形的頂角度數(shù)為 。
A
B
E
D
F
C
5���、如圖����,已知BE⊥AD��,CF⊥AD��,且BE=CF�,判斷AD是△ABC的中線還是角平分線?
說明你的理由�����。
7、
三����、應(yīng)用深化
三、看我有多棒
1��、在△ABC和△中����,①AB=②BC=③AC=④∠A=∠⑤∠B=∠⑥∠C=∠,下列條件中��,不能保證△ABC≌△的是( ) A①②③ B①②⑤ C②④⑤ D①③⑤
2�����、(1)某等腰三角形的兩條邊長分別為3cm和6cm����,則它的周長為 �����。
(2)等腰三角形的周長為13cm,其中一邊長為3cm�,則該等腰三角形的腰長為 。
3�����、如圖1線段AC與BD交于點O����,且OA=OC,請?zhí)砑右粋€條件 �,使△OAB≌△OCD
A
B
C
D
圖2
8、4�、如圖2,△ABC中AB=AC�����,點D在AC上���,且BD=BC=AD�����,則∠A的度數(shù)為
D
C
O
A
B
圖1
5����、已知等腰三角形的兩內(nèi)角的度數(shù)之比為1:4,則這個等腰三角形的頂角度數(shù)為
6��、如圖3�,A、B�����、F�����、D在同一直線上�����,AB=DF�����,AE=BC��,且AE∥BC�����。
求證:⑴△AEF≌△BCD��,
A
B
F
D
E
C
圖3
⑵EF∥CD
中考真題:已知:如圖��,△ABC中�,AD是高,CE是中線���,DC=BE, DG⊥CE,G是垂足���,
求證:(1)G是CE中點(2)∠B=2∠BCE
隨時糾錯
三、小結(jié)反饋
學(xué)而不思則罔����,本節(jié)課我的反思:
課后反思
 九年級數(shù)學(xué)上冊第一章你能證明它們嗎導(dǎo)學(xué)案1無答案北師大版
九年級數(shù)學(xué)上冊第一章你能證明它們嗎導(dǎo)學(xué)案1無答案北師大版