《2018屆中考數(shù)學全程演練 第二部分 圖形與幾何 第八單元 四邊形 第26課時 多邊形及其內(nèi)角和》由會員分享，可在線閱讀，更多相關(guān)《2018屆中考數(shù)學全程演練 第二部分 圖形與幾何 第八單元 四邊形 第26課時 多邊形及其內(nèi)角和（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

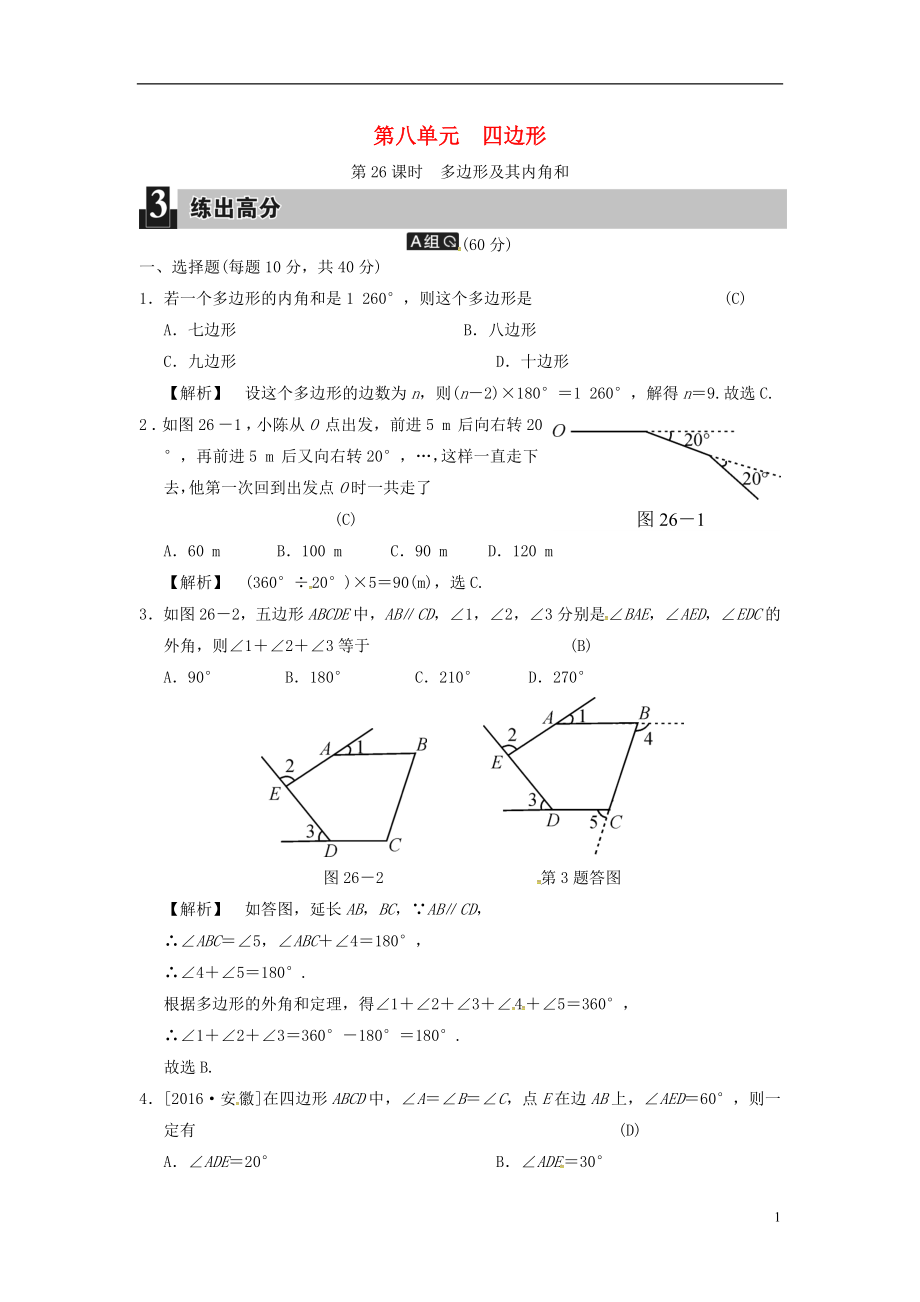
1、 第八單元 四邊形 第26課時　多邊形及其內(nèi)角和 (60分) 一、選擇題(每題10分，共40分) 1．若一個多邊形的內(nèi)角和是1 260°，則這個多邊形是 (C) A．七邊形 B．八邊形 C．九邊形 D．十邊形 【解析】　設(shè)這個多邊形的邊數(shù)為n，則(n－2)×180°＝1 260°，解得n＝9.故選C. 圖26－1 2．如圖26－1，小陳從O點出發(fā)，前進5 m后向右轉(zhuǎn)20°，再前進5 m后又向右轉(zhuǎn)20°，…，這樣一直走下去，他第一次回到出發(fā)點O時一共走了 (C) A．60 m B．100 m

2、 C．90 m D．120 m 【解析】　(360°÷20°)×5＝90(m)，選C. 3．如圖26－2，五邊形ABCDE中，AB∥CD，∠1，∠2，∠3分別是∠BAE，∠AED，∠EDC的外角，則∠1＋∠2＋∠3等于 (B) A．90°　　　　B．180°　　　　C．210°　　　D．270° 圖26－2 　　第3題答圖 【解析】　如答圖，延長AB，BC，∵AB∥CD， ∴∠ABC＝∠5，∠ABC＋∠4＝180°， ∴∠4＋∠5＝180°. 根據(jù)多邊形的外角和定理，得∠1＋∠2＋∠3＋∠4＋∠5＝360°，

3、 ∴∠1＋∠2＋∠3＝360°－180°＝180°. 故選B. 4．[2016·安徽]在四邊形ABCD中，∠A＝∠B＝∠C，點E在邊AB上，∠AED＝60°，則一定有 (D) A．∠ADE＝20° B．∠ADE＝30° C．∠ADE＝∠ADC D．∠ADE＝∠ADC 【解析】　利用三角形的內(nèi)角和為180°，四邊形的內(nèi)角和為360°，分別表示出∠A，∠B，∠C，根據(jù)∠A＝∠B＝∠C，得到∠ADE＝∠EDC，因為∠ADC＝∠ADE＋∠EDC＝∠EDC＋∠EDC＝∠EDC，所以∠ADE＝∠ADC. 二、填空題(每題10分，共2

4、0分) 5．[2016·巴中]若一個正多邊形的一個外角等于30°，則這個多邊形為正__12__邊形． 6．[2017·自貢]一個多邊形的內(nèi)角和比它的外角和的3倍少180°，則它的邊數(shù)是__7__． (10分) 圖26－3 7．(10分)[2016·杭州模擬]如圖26－3，已知四邊形ABCD中，∠C＝72°，∠D＝81°.沿EF折疊四邊形，使點A，B分別落在四邊形內(nèi)部的點A′，B′處，則∠1＋∠2＝__54°__. 【解析】　連結(jié)AA′，BB′. 第7題答圖 由題意得∠1＋∠2＋∠FEA′＋∠EFB′＋∠D＋∠C＝360°， 又∵∠C＝72°，∠D＝81°， ∴∠FEA′＋∠

5、EFB′＋∠1＋∠2＝207°； 又∵∠AEF＋∠BFE＋∠FEA′＋∠EFB′＋∠1＋∠2＝360°，四邊形A′B′FE是四邊形ABFE翻轉(zhuǎn)得到的， ∴∠FEA′＋∠EFB′＝∠AEF＋∠BFE， ∴∠FEA′＋∠EFB′＝153°， ∴∠1＋∠2＝54°. (30分) 8．(30分)(1)問題發(fā)現(xiàn)：如圖26－4①，△ACB和△DCE均為等邊三角形，點A，D，E在同一直線上，連結(jié)BE. 填空：①∠AEB的度數(shù)為__60°__； ②線段AD，BE之間的數(shù)量關(guān)系為__相等__； (2)拓展探究：如圖26－4②，△ACB和△DCE均為等 腰直角三角形，∠ACB＝∠DCE＝90°

6、，點A，D，E在同一直線上，CM為△DCE中DE邊上的高，連結(jié)BE，請判斷∠AEB的度數(shù)及線段CM，AE，BE之間的數(shù)量關(guān)系，并說明理由． 圖26－4 解：(1)∵∠ACB＝∠DCE，∠DCB＝∠DCB， ∴∠ACD＝∠BCE， 在△ACD和△BCE中， ∴△ACD≌△BCE(SAS)， ∴AD＝BE，∠CEB＝∠ADC＝180°－∠CDE＝120°， ∴∠AEB＝∠CEB－∠CED＝60°； (2)∠AEB＝90°，AE＝BE＋2CM， 理由如下： ∵△ACB和△DCE均為等腰直角三角形， ∴CA＝CB，CD＝CE，∠ACB＝∠DCE＝90°， ∵∠ACD＋∠DCB＝90°＝∠DCB＋∠BCE， ∴∠ACD＝∠BCE， ∴△ACD≌△BCE(SAS)， ∴AD＝BE，∠ADC＝∠BEC. ∵△DCE為等腰直角三角形， ∴∠CDE＝∠CED＝45°， ∵點A，D，E在同一直線上， ∴∠ADC＝135°. ∴∠BEC＝135°， ∴∠AEB＝∠BEC－∠CED＝90°. ∵CD＝CE，CM⊥DE， ∴DM＝ME. ∵∠DCE＝90°， ∴DM＝ME＝CM， ∴AE＝AD＋DE＝BE＋2CM. 3