《2020版新教材高中物理 主題2 機械振動與機械波 2 簡諧運動的描述學案 新人教版必修第一冊》由會員分享����,可在線閱讀�,更多相關(guān)《2020版新教材高中物理 主題2 機械振動與機械波 2 簡諧運動的描述學案 新人教版必修第一冊(7頁珍藏版)》請在裝配圖網(wǎng)上搜索��。
1�����、2 簡諧運動的描述
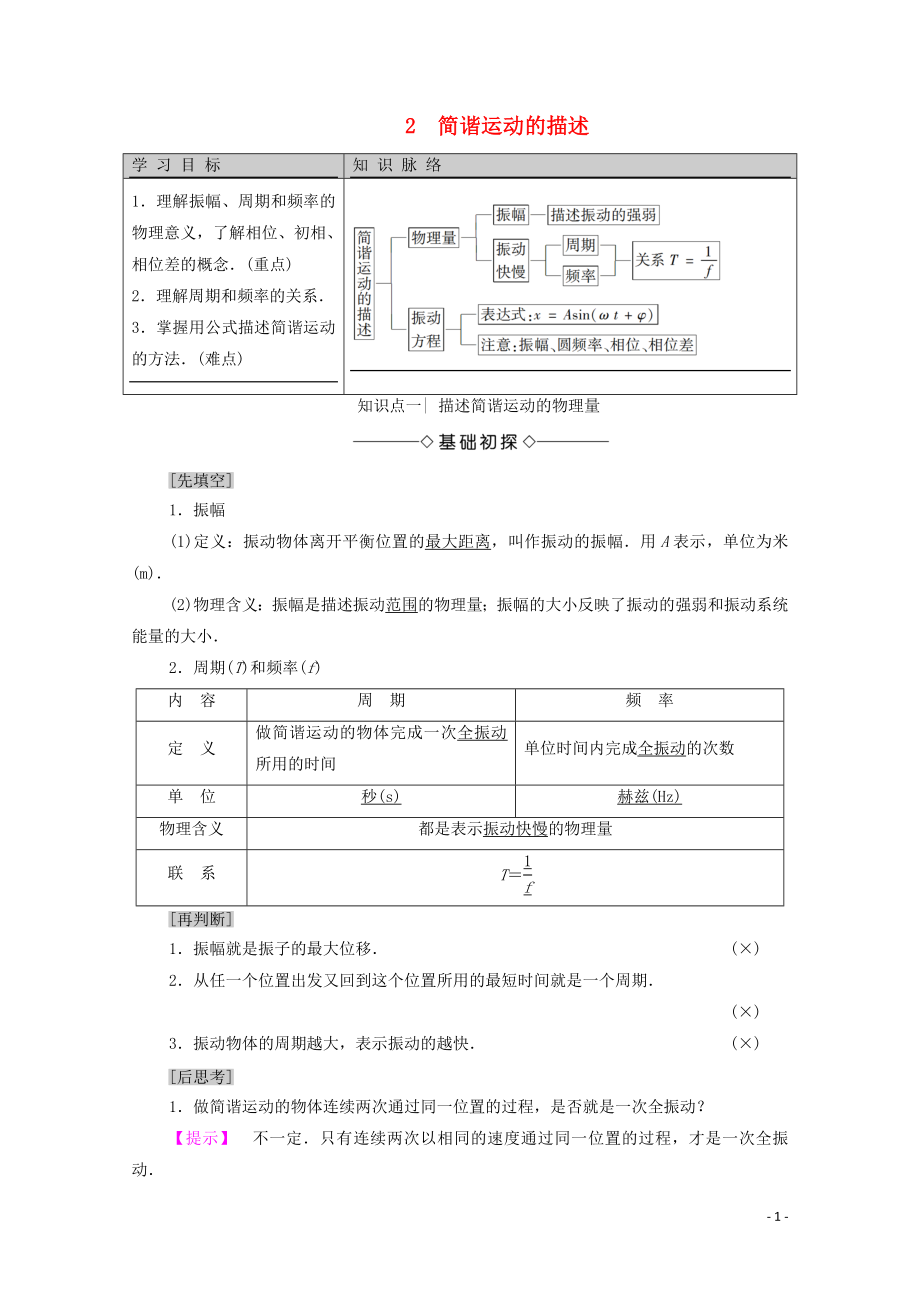
學 習 目 標
知 識 脈 絡
1.理解振幅��、周期和頻率的物理意義��,了解相位��、初相����、相位差的概念.(重點)
2.理解周期和頻率的關(guān)系.
3.掌握用公式描述簡諧運動的方法.(難點)
知識點一| 描述簡諧運動的物理量
1.振幅
(1)定義:振動物體離開平衡位置的最大距離,叫作振動的振幅.用A表示�����,單位為米(m).
(2)物理含義:振幅是描述振動范圍的物理量����;振幅的大小反映了振動的強弱和振動系統(tǒng)能量的大小.
2.周期(T)和頻率(f)
內(nèi) 容
周 期
頻 率
定 義
做簡諧運動的物體完成一次全振動所用的時間
單位時間內(nèi)完成全振動的次數(shù)
2�、
單 位
秒(s)
赫茲(Hz)
物理含義
都是表示振動快慢的物理量
聯(lián) 系
T=
1.振幅就是振子的最大位移. (×)
2.從任一個位置出發(fā)又回到這個位置所用的最短時間就是一個周期.
(×)
3.振動物體的周期越大,表示振動的越快. (×)
1.做簡諧運動的物體連續(xù)兩次通過同一位置的過程�����,是否就是一次全振動�?
【提示】 不一定.只有連續(xù)兩次以相同的速度通過同一位置的過程,才是一次全振動.
2.如果改變彈簧振子的振幅�����,其振動的周期是否會改變呢�����?彈簧振子的周期與什么因素有關(guān)呢�����?我們可以提出哪些猜想�����?怎樣設計一個實驗來驗證這個猜想�����?
【提示】 猜想:影響彈
3、簧振子周期的因素可能有:振幅��、振子的質(zhì)量����、彈簧的勁度系數(shù)等.我們可以設計這樣一個實驗:彈簧一端固定,彈簧的另一端連著有孔小球�����,使小球在光滑的水平桿上滑動.通過改變振幅��、振子的質(zhì)量和彈簧的勁度系數(shù)�,測量不同情況下振子的周期,注意在改變一個物理量的時候其他物理量應保持不變.
1.振幅與位移�、路程����、周期的關(guān)系
(1)振幅與位移:振動中的位移是矢量�,振幅是標量.在數(shù)值上��,振幅與振動物體的最大位移相等�����,在同一簡諧運動中振幅是確定的,而位移隨時間做周期性的變化.
(2)振幅與路程:振動中的路程是標量�����,是隨時間不斷增大的.其中常用的定量關(guān)系是:一個周期內(nèi)的路程為4倍振幅,半個周期內(nèi)的路程為2倍
4、振幅.
(3)振幅與周期:在簡諧運動中����,一個確定的振動系統(tǒng)的周期(或頻率)是固定的�,與振幅無關(guān).
2.對全振動的理解
(1)全振動的定義:振動物體以相同的速度相繼通過同一位置所經(jīng)歷的過程,叫作一次全振動.
(2)正確理解全振動的概念��,還應注意把握全振動的四個特征.
①物理量特征:位移(x)�、加速度(a)�����、速度(v)三者第一次同時與初始狀態(tài)相同.
②時間特征:歷時一個周期.
③路程特征:振幅的4倍.
④相位特征:增加2π.
1.如圖所示,彈簧振子以O點為平衡位置�,在B��,C間振動����,則( )
A.從B→O→C→O→B為一次全振動
B.從O→B→O→C→B為一次全振動
5、
C.從C→O→B→O→C為一次全振動
D.OB不一定等于OC
E.B����、C兩點是關(guān)O點對稱的
解析:O點為平衡位置,B����,C為兩側(cè)最遠點,則從B起經(jīng)O,C,O���,B的路程為振幅的4倍��,即A正確�;若從O起經(jīng)B���,O�����,C��,B的路程為振幅的5倍����,超過一次全振動,即B錯誤�����;若從C起經(jīng)O���,B��,O�,C的路程為振幅的4倍�����,即C正確�����;因彈簧振子的系統(tǒng)摩擦不考慮��,所以它的振幅一定�,即D錯誤��,E正確.
答案:ACE
2.一個物體做簡諧運動時���,周期是T����,振幅是A,那么物體( )
A.在任意內(nèi)通過的路程一定等于A
B.在任意內(nèi)通過的路程一定等于2A
C.在任意內(nèi)通過的路程一定等于3A
D.在任意T內(nèi)通過
6����、的路程一定等于4A
E.在任意T內(nèi)通過的位移一定為零
解析:物體做簡諧運動,是變加速直線運動�,在任意內(nèi)通過的路程不一定等于A,故A錯誤��;物體做簡諧運動�����,在任意內(nèi)通過的路程一定等于2A�����,故B正確���;物體做簡諧運動���,在任意內(nèi)通過的路程不一定等于3A���,故C錯誤;物體做簡諧運動��,在一個周期內(nèi)完成一次全振動���,位移為零�,路程為4A��,故D�、E正確.
答案:BDE
3.彈簧振子以O點為平衡位置在B、C兩點間做簡諧運動�����,BC相距20 cm�,某時刻振子處于B點,經(jīng)過0.5 s���,振子首次到達C點.求:
(1)振子的振幅;
(2)振子的周期和頻率�;
(3)振子在5 s內(nèi)通過的路程大小.
解析:(1)設振
7�����、幅為A,則有2A=BC=20 cm����,所以A=10 cm.
(2)從B首次到C的時間為周期的一半,因此T=2t=1 s����;再根據(jù)周期和頻率的關(guān)系可得f==1 Hz.
(3)振子一個周期通過的路程為4A=40 cm,則5 s內(nèi)通過的路程為s=·4A=5×40 cm=200 cm.
答案:(1)10 cm (2)1 s 1 Hz (3)200 cm.
振幅與路程的關(guān)系
振動中的路程是標量����,是隨時間不斷增大的.一個周期內(nèi)的路程為4倍的振幅,半個周期內(nèi)的路程為2倍的振幅.
(1)若從特殊位置開始計時����,如平衡位置、最大位移處��,周期內(nèi)的路程等于振幅.
(2)若從一般位置開始計時�����,周期內(nèi)的路程
8、與振幅之間沒有確定關(guān)系���,路程可能大于�、等于或小于振幅.
知識點二| 簡諧運動的表達式
1.表達式:簡諧運動的表達式可以寫成
x=Asin或x=Asin(t+φ)
2.表達式中各量的意義
(1)“A”表示簡諧運動的“振幅”.
(2)ω是一個與頻率成正比的物理量叫簡諧運動的圓頻率.
(3)“T”表示簡諧運動的周期���,“f”表示簡諧運動的頻率�����,它們之間的關(guān)系為T=.
(4)“t+φ”或“2πft+φ”表示簡諧運動的相位.
(5)“φ”表示簡諧運動的初相位���,簡稱初相.
1.簡諧運動的位移表達式與計時時刻物體所在位置無關(guān). (×)
2.一個物體運動時其相位變化2π,就
9��、意味著完成一次全振動. (√)
3.簡諧運動的表達式x=Asin(ωt+φ)中�,ωt+φ的單位是弧度. (√)
1.有兩個簡諧運動:x1=3asin和x2=9asin ,它們的振幅之比是多少�?頻率各是多少?
【提示】 它們的振幅分別為3a和9a����,比值為1∶3;頻率分別為2b和4b.
2.簡諧運動的相位差Δφ=φ2-φ1的含義是什么�?
【提示】 兩個簡諧運動有相位差,說明其步調(diào)不相同�����,例如甲和乙兩個簡諧運動的相位差為π����,意味著乙總比甲滯后個周期或次全振動.
1.簡諧運動的表達式:x=Asin(ωt+φ)
式中x表示振動質(zhì)點相對于平衡位置的位移;t表示振動的時間���;A表示振
10�����、動質(zhì)點偏離平衡位置的最大距離��,即振幅.
2.各量的物理含義
(1)圓頻率:表示簡諧運動物體振動的快慢.與周期T及頻率f的關(guān)系:ω==2πf.
(2)φ表示t=0時�,簡諧運動質(zhì)點所處的狀態(tài)�,稱為初相位或初相.ωt+φ表示做簡諧運動的質(zhì)點在t時刻處在一個運動周期中的哪個狀態(tài),所以表示簡諧運動的相位.
3.做簡諧運動的物體運動過程中的對稱性
(1)瞬時量的對稱性:各物理量關(guān)于平衡位置對稱.以水平彈簧振子為例����,振子通過關(guān)于平衡位置對稱的兩點,位移�����、速度、加速度大小相等�����,動能����、勢能、機械能相等.
(2)過程量的對稱性:振動質(zhì)點來回通過相同的兩點間的時間相等��,如tB C=tC B��;質(zhì)點經(jīng)過
11�、關(guān)于平衡位置對稱的等長的兩線段的時間相等,如tB C=tB′C′�,如圖所示.
4.做簡諧運動的物體運動過程中的周期性
簡諧運動是一種周而復始的周期性的運動,按其周期性可做如下判斷:
(1)若t2-t1=nT�,則t1,t2兩時刻振動物體在同一位置�����,運動情況相同.
(2)若t2-t1=nT+T�,則t1����,t2兩時刻�����,描述運動的物理量(x��,F(xiàn)���,a,v)均大小相等�,方向相反.
(3)若t2-t1=nT+T或t2-t1=nT+T,則當t1時刻物體到達最大位移處時���,t2時刻物體到達平衡位置����;當t1時刻物體在平衡位置時����,t2時刻物體到達最大位移處;若t1時刻物體在其他位置���,t2時刻物體到達何處就要視
12��、具體情況而定.
4.一位游客在千島湖邊欲乘坐游船�����,當日風浪較大����,游船上下浮動.可把游船浮動簡化成豎直方向的簡諧運動,振幅為20 cm�����,周期為3.0 s.當船上升到最高點時��,甲板剛好與碼頭地面平齊.地面與甲板的高度差不超過10 cm時��,游客能舒服地登船.在一個周期內(nèi)����,游客能舒服登船的時間是________.
解析:由于振幅A為20 cm,振動方程為y=Asin ωt(平衡位置計時���,ω=)����,由于高度差不超過10 cm,游客能舒服地登船�����,代入數(shù)據(jù)可知�����,在一個振動周期內(nèi)����,臨界時刻為t1=����,t2=,所以在一個周期內(nèi)舒服登船的時間為Δt=t2-t1==1.0 s.
答案:1.0 s
5.物體A
13�、做簡諧運動的振動位移xA=3sin m,物體B做簡諧運動的振動位移xB=5sin m.比較A���,B的運動( )
A.振幅是矢量����,A的振幅是6 m,B的振幅是10 m
B.周期是標量��,A�,B周期相等,為100 s
C.A振動的頻率fA等于B振動的頻率fB
D.A振動的圓頻率ωA等于B振動的圓頻率ωB
E.A的相位始終超前B的相位
解析:振幅是標量����,A,B的振幅分別是3 m�����,5 m�����,A錯����;A,B的圓頻率ω=100�����,周期T== s=6.28×10-2 s,B錯�����,D對����;因為TA=TB,故fA=fB�,C對;Δφ=φAO-φBO=為定值���,E對.
答案:CDE
6.一物體沿x軸做簡諧運動,振
14���、幅為8 cm�,頻率為0.5 Hz��,在t=0時�,位移是4 cm,且向x軸負方向運動�����,試寫出用正弦函數(shù)表示的振動方程�����,并畫出相應的振動圖象.
解析:簡諧運動的表達式為x=Asin(ωt+φ),根據(jù)題目所給條件得A=8 cm���,ω=2πf=π��,所以x=8sin(πt+φ) cm�����,將t=0�,x0=4 cm代入得4=8sin φ�,解得初相φ=或φ=π,因為t=0時���,速度方向沿x軸負方向���,即位移在減小,所以取φ=π��,所求的振動方程為x=8sin(πt+π) cm���,畫對應的振動圖象如圖所示.
答案:見解析
用簡諧運動表達式解答振動問題的方法
(1)明確表達式中各物理量的意義���,可直接讀出振幅����、圓頻率�����、初相.
(2)ω==2πf是解題時常涉及到的表達式.
(3)解題時畫出其振動圖象����,會使解答過程簡捷、明了.
- 7 -
 2020版新教材高中物理 主題2 機械振動與機械波 2 簡諧運動的描述學案 新人教版必修第一冊
2020版新教材高中物理 主題2 機械振動與機械波 2 簡諧運動的描述學案 新人教版必修第一冊