《2022高中數(shù)學 第2章 平面解析幾何初步 第二節(jié) 圓與方程2 直線與圓的位置關系學案 蘇教版必修2》由會員分享，可在線閱讀，更多相關《2022高中數(shù)學 第2章 平面解析幾何初步 第二節(jié) 圓與方程2 直線與圓的位置關系學案 蘇教版必修2（4頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、2022高中數(shù)學 第2章 平面解析幾何初步 第二節(jié) 圓與方程2 直線與圓的位置關系學案 蘇教版必修2 一、考點突破 知識點 課標要求 題型 說明 直線與圓的位置關系 1. 掌握直線與圓的位置關系的兩種判定方法； 2. 能利用圓心到直線的距離、半弦長、圓的半徑三者之間的關系，解有關弦長的問題； 3. 理解一元二次方程根的判定及根與系數(shù)關系，并能利用它們解一些簡單的直線與圓的關系問題 選擇題 填空題 本節(jié)課的核心是“如何用‘數(shù)’的關系來判斷直線與圓的位置關系”，學會從不同角度分析思考問題，為后續(xù)學習打下基礎。為此，可類比直線與直線的交點坐標的求法，讓學生認識到用解析法解

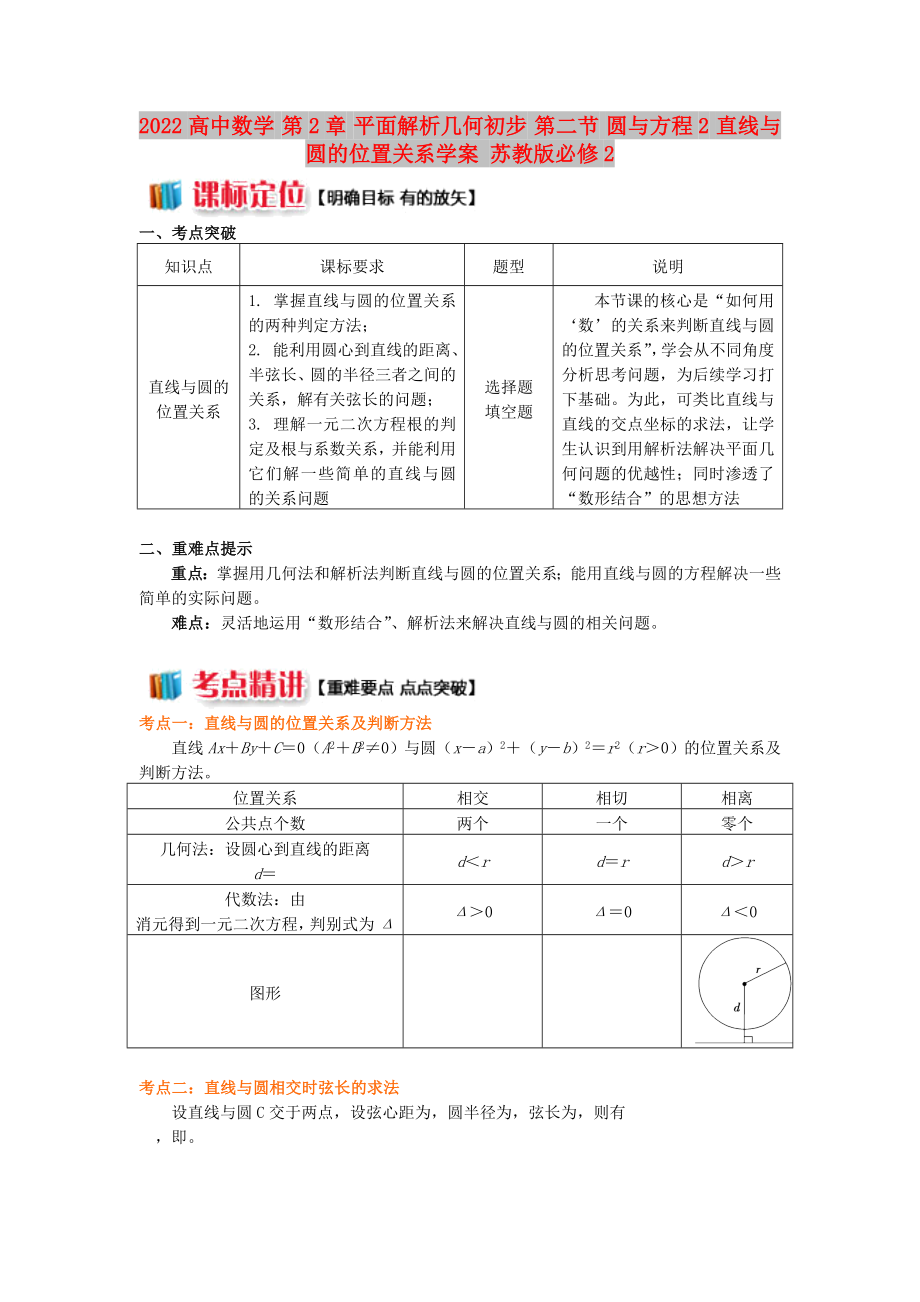
2、決平面幾何問題的優(yōu)越性；同時滲透了“數(shù)形結合”的思想方法 二、重難點提示 重點：掌握用幾何法和解析法判斷直線與圓的位置關系；能用直線與圓的方程解決一些簡單的實際問題。 難點：靈活地運用“數(shù)形結合”、解析法來解決直線與圓的相關問題。 考點一：直線與圓的位置關系及判斷方法 直線Ax＋By＋C＝0（A2＋B2≠0）與圓（x－a）2＋（y－b）2＝r2（r＞0）的位置關系及判斷方法。 位置關系 相交 相切 相離 公共點個數(shù) 兩個 一個 零個 幾何法：設圓心到直線的距離 d＝ d＜r d＝r d＞r 代數(shù)法：由 消元得到一元二次方程，判別式為Δ Δ＞

3、0 Δ＝0 Δ＜0 圖形 考點二：直線與圓相交時弦長的求法 設直線與圓C交于兩點，設弦心距為，圓半徑為，弦長為，則有 ，即。 考點三：直線與圓相切時切線的求法 1. 求斜率為（為常數(shù)）的切線方程 設切線的方程為，利用圓心到直線的距離等于半徑列出方程求。 2. 求過一點的圓的切線方程 首先判斷這點與圓的位置關系，看點在圓外還是圓上。 ① 若點在圓上，則連接圓心和該點的直線與切線垂直，利用垂直關系確定切線的斜率，從而確定切線方程；若切線的斜率不存在，其切線方程也確定了。 ② 若點在圓外，求切線時常用以下方法： A. 設切線斜率，寫出切線方程，利用

4、判別式等于零求斜率； B. 設切線斜率，利用圓心到直線的距離等于半徑求斜率； C. 設切點坐標，則利用切線方程來求解。 例題1 （直線與圓位置關系的判斷） 如圖所示，已知直線l：y＝kx＋5與圓C：（x－1）2＋y2＝1。 （1）當k為何值時，直線l與圓C相交？ （2）當k為何值時，直線l與圓C相切？ （3）當k為何值時，直線l與圓C相離？ 思路分析：思路一：聯(lián)立l及C的方程一元二次方程直線與圓的關系； 思路二：求圓心到直線l的距離d―→比較d與半徑1的大小下結論。 答案：方法一　由，消去y，得（x－1）2＋（kx＋5）2＝1， 即（k2＋1）x2＋（10k－

5、2）x＋25＝0， 則Δ＝（10k－2）2－4×25（k2＋1）＝－96－40k。 （1）當Δ>0，即k<－時，直線l與圓C相交。 （2）當Δ＝0，即k＝－時，直線l與圓C相切。 （3）當Δ<0，即k>－時，直線l與圓C相離。 方法二　圓C的圓心C（1，0），半徑r＝1，由點到直線的距離公式得圓心C到直線l的距離d＝。 （1）當<1，即k<－時，直線l與圓C相交。 （2）當＝1，即k＝－時，直線l與圓C相切。 （3）當>1，即k>－時，直線l與圓C相離。 技巧點撥：直線與圓位置關系判斷的三種方法 （1）幾何法：由圓心到直線的距離d與圓的半徑r的大小關系判斷。 （2）代數(shù)

6、法：根據(jù)直線與圓的方程組成的方程組解的個數(shù)來判斷。 （3）直線系法：若直線恒過定點，可通過判斷點與圓的位置關系判斷，但有一定的局限性，必須是過定點的直線系。 例題2 （直線與圓的相交弦問題） 求直線l：3x＋y－6＝0被圓C：x2＋y2－2y－4＝0截得的弦長。 思路分析：方程組→解出交點坐標→兩點間距離即弦長或方程組→得x1＋x2與x1·x2 →弦長公式求弦長或圓心到直線的距離→構造直角三角形求弦長。 答案：方法一　由， 得交點A（1，3），B（2，0）， ∴弦AB的長為AB＝＝。 方法二　由 消去y得x2－3x＋2＝0。 設兩交點A、B的坐標分別為A（x1，y1）

7、、B（x2，y2） 則由根與系數(shù)的關系得x1＋x2＝3，x1·x2＝2。 ∴|AB|＝ ＝ ＝ ＝ ＝＝， 即弦AB的長為。 方法三　圓C：x2＋y2－2y－4＝0可化為x2＋（y－1）2＝5，其圓心坐標（0，1），半徑r＝，點（0，1）到直線l的距離為d＝＝，所以半弦長為＝＝ ＝， 所以弦長AB＝。 技巧點撥： 對于弦長問題，常利用第三種方法，即利用半弦長、弦心距、半徑構成的直角三角形，通過數(shù)形結合，利用勾股定理來求解。 　 忽略直線斜率不存在的情況致誤 例題 已知圓M：（x－1）2＋（y－1）2＝4，直線a過點P（2，3）且與圓M交于A，B兩點，且AB

8、＝2，求直線a的方程。 【錯解】設直線a的方程為y－3＝k（x－2），即kx－y＋3－2k＝0。 如圖所示，作MC⊥AB于C，在直角三角形MBC中， BC＝，MB＝2，MC＝＝1， 由點到直線的距離公式得點M（1，1）到直線a的距離為＝1， 解得k＝， 所以直線a的方程為3x－4y＋6＝0。 【錯因分析】錯解忽略了直線a的斜率不存在的情況。 【防范措施】點斜式方程并不能表示出斜率不存在的情況，故在求直線方程時，若設點斜式方程，根據(jù)條件求得斜率后，應注意驗證斜率不存在的情況是否滿足題意。本題就是忽略了斜率不存在的特殊情況而出錯的。 【正解】①當直線a的斜率存在時，設直線a的方程為y－3＝k（x－2），即kx－y＋3－2k＝0。 如圖所示，作MC⊥AB于C，在直角三角形MBC中， BC＝，MB＝2，MC＝＝1， 由點到直線的距離公式得點M（1，1）到直線a的距離為＝1， 解得k＝， 所以直線a的方程為3x－4y＋6＝0。 ②當直線a的斜率不存在時，其方程為x＝2， 圓心到此直線的距離也是1，所以符合題意。 綜上，直線a的方程為3x－4y＋6＝0或x＝2。