《2020年秋六年級數(shù)學上冊 4.3 一元一次方程的應用學案2（無答案） 魯教版五四制》由會員分享，可在線閱讀，更多相關《2020年秋六年級數(shù)學上冊 4.3 一元一次方程的應用學案2（無答案） 魯教版五四制（3頁珍藏版）》請在裝配圖網上搜索。

1、 4.3 一元一次方程的應用（2） 1、會找等積變形問題類型應用題的相等關系設未知數(shù)列方程； 2、掌握用方程解決實際問題的基本步驟：理解題意，尋找等量關系，設未知數(shù)列方程，解方程，作答. 重點：列方程解決等積問題． 難點：將實際問題轉化成一元一次方程來解決． 1、借助表格分析應用題，列方程解決實際問題； 2、在探索的過程中積極動手、動腦、動口，加強交流互助，達到合作共贏． 1、圓柱的底面半徑為r，高為h，那么圓柱的底面面積是_______，圓柱的體積是_______.如果一個圓柱的底面直徑是10cm，高為h，則圓柱的體積可表示為

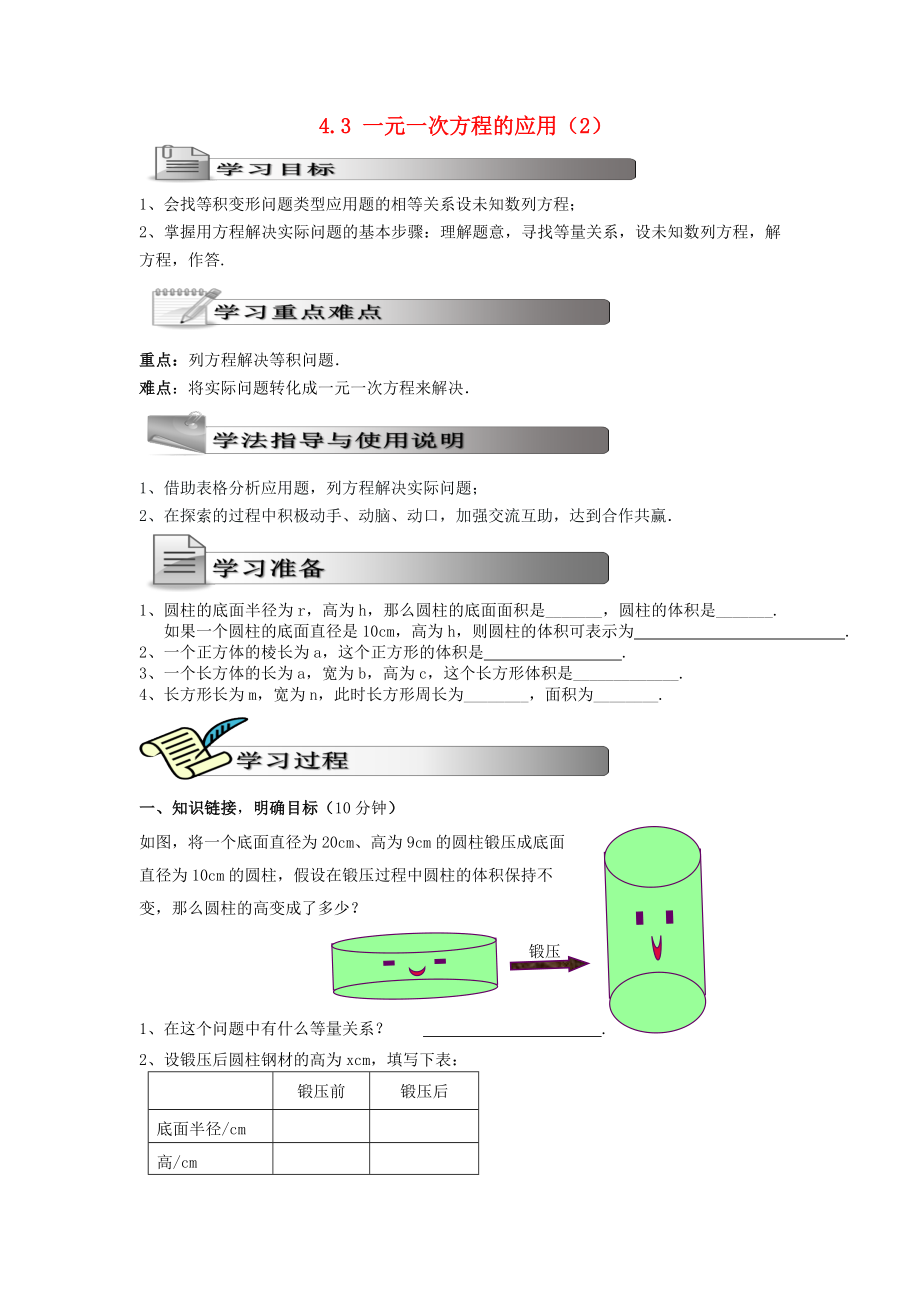
2、 . 2、一個正方體的棱長為a，這個正方形的體積是 . 3、一個長方體的長為a，寬為b，高為c，這個長方形體積是_____________. 4、長方形長為m，寬為n，此時長方形周長為________，面積為________. 一、知識鏈接，明確目標（10分鐘） 如圖，將一個底面直徑為20cm、高為9cm的圓柱鍛壓成底面 直徑為10cm的圓柱，假設在鍛壓過程中圓柱的體積保持不 變，那么圓柱的高變成了多少？ 鍛壓 1、在這個問題中有什么等量關系？ . 2、設鍛壓后圓

3、柱鋼材的高為xcm，填寫下表： 鍛壓前 鍛壓后 底面半徑/cm 高/cm 體積/cm3 根據(jù)等量關系，列出方程： . 解這個方程，得x= . 因此，高變成了 cm. 【溫馨提示】1、如果題目沒有要求，在表示圓的周長或面積、圓柱圓錐的體積時保留π的形式。 2、解方程時要注意選擇簡單的方法 鞏固練習： 要鍛造一個直徑為10cm，高為8cm的圓柱形毛坯，應截取直徑為8cm的圓鋼多長？ 小結：列方程解應用題的一般步驟是： 、

4、 、 、 、 、 . 二、自主學習，點撥釋疑（限時15分鐘） 【 例1 】用一根長為10m的鐵絲圍成一個長方形. 探究（1）使得這個長方形的長比寬多1.4m，此時長方形的長、寬各為多少米？ 【分析】由題意知，長方形的 始終是不變的， 所以可得等量關系 = 在解決這個問題的過程中，要抓住這個等量關系。 解：（1）設此時長方形的 為xm，則它的 為 m，由題意得 探究（2）使得這個長方形的長比寬多0.8m，此時長方形的長、寬各為多少

5、米？ 解： 探究（3）使得這個長方形的長與寬相等，即圍成一個正方形，此時正方形的邊長是多少米？ 解后反思：1、本題列方程時用的等量關系是什么？ 2、在表示未知量時抓住關鍵字：“多、少、倍、分、比”. 三、鞏固練習，提升能力（限時5分鐘） 1、第一塊試驗田的面積比第二塊試驗田的3倍還多100平方米，這兩塊試驗田共2900平方米，兩塊試驗田的面積分別是_________和________平方米。 2、用直徑4cm的圓鋼鑄造3個直徑為2cm、高為16cm的圓柱形零件，求需要截取多長的圓鋼？ ※3、一塊長、寬、高分別為9cm、7cm、3c

6、m的長方體鐵塊和一塊棱長為5cm的正方體鐵塊熔鍛成一個圓柱體，其底面直徑為20cm，試求圓柱體的高. 四、拓展延伸 ※已知一圓柱形容器底面半徑為0.5m,高線長為1.5m,里面盛有1m深的水，將底面半徑為0.3m，高線長為0.5m的圓柱形鐵塊沉入水中，問容器內水面將升高多少? 五、歸納總結，反思矯正（暢所欲言，3分鐘） 1． 列方程解應用題的一般步驟是什么？關鍵是什么？ 2． 本節(jié)的學習活動，你有哪些收獲？還有什么疑惑？ 六、課堂檢測，反饋糾錯（限時6分鐘） 1、用直徑為40cm、長為1m的圓鋼，能拉成直徑為4cm、長為_______m的鋼絲。 2、用一根鐵絲可圍成一個長10厘米、寬6厘米的長方形。若將它圍成一個正方形，則這個正方形的面積是（ ） A．100㎝2 B．24㎝2 C．64㎝2 D．256㎝2 思考題：小明的爸爸想用10米鐵線在墻邊圍成一個菜地，使長比寬大4米，問小明要幫他爸爸圍成的菜地的長和寬各是多少呢？ 六、布置作業(yè)，鞏固提升 1、整理導學案 2、課本p139 第 3題 學后反思：