《山東省臨沐縣青云中學(xué)2012-2013學(xué)年八年級(jí)數(shù)學(xué)下冊(cè) 第十九章 矩形的性質(zhì)學(xué)案（無(wú)答案） 新人教版》由會(huì)員分享，可在線閱讀，更多相關(guān)《山東省臨沐縣青云中學(xué)2012-2013學(xué)年八年級(jí)數(shù)學(xué)下冊(cè) 第十九章 矩形的性質(zhì)學(xué)案（無(wú)答案） 新人教版（2頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

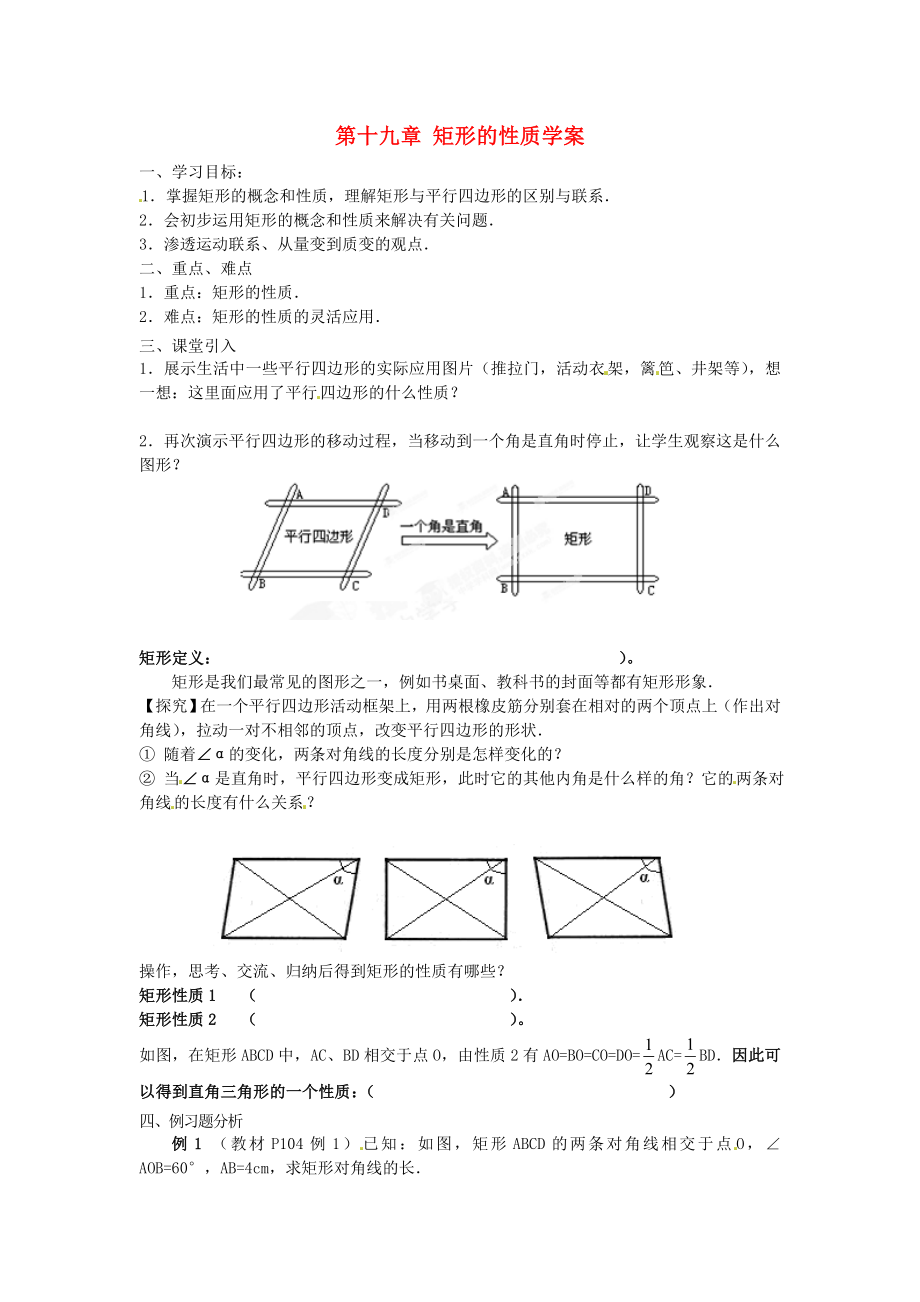
1、第十九章 矩形的性質(zhì)學(xué)案 一、學(xué)習(xí)目標(biāo)： 1．掌握矩形的概念和性質(zhì)，理解矩形與平行四邊形的區(qū)別與聯(lián)系． 2．會(huì)初步運(yùn)用矩形的概念和性質(zhì)來(lái)解決有關(guān)問(wèn)題． 3．滲透運(yùn)動(dòng)聯(lián)系、從量變到質(zhì)變的觀點(diǎn)． 二、重點(diǎn)、難點(diǎn) 1．重點(diǎn)：矩形的性質(zhì)． 2．難點(diǎn)：矩形的性質(zhì)的靈活應(yīng)用． 三、課堂引入 1．展示生活中一些平行四邊形的實(shí)際應(yīng)用圖片（推拉門，活動(dòng)衣架，籬笆、井架等），想一想：這里面應(yīng)用了平行四邊形的什么性質(zhì)？ 2．再次演示平行四邊形的移動(dòng)過(guò)程，當(dāng)移動(dòng)到一個(gè)角是直角時(shí)停止，讓學(xué)生觀察這是什么圖形？ 矩形定義：

2、 ）。 矩形是我們最常見(jiàn)的圖形之一，例如書桌面、教科書的封面等都有矩形形象． 【探究】在一個(gè)平行四邊形活動(dòng)框架上，用兩根橡皮筋分別套在相對(duì)的兩個(gè)頂點(diǎn)上（作出對(duì)角線），拉動(dòng)一對(duì)不相鄰的頂點(diǎn)，改變平行四邊形的形狀． ① 隨著∠α的變化，兩條對(duì)角線的長(zhǎng)度分別是怎樣變化的？ ② 當(dāng)∠α是直角時(shí)，平行四邊形變成矩形，此時(shí)它的其他內(nèi)角是什么樣的角？它的兩條對(duì)角線的長(zhǎng)度有什么關(guān)系？ 操作，思考、交流、歸納后得到矩形的性質(zhì)有哪些？ 矩形性質(zhì)1　 （ ）． 矩形性質(zhì)2　 （

3、 ）。 如圖，在矩形ABCD中，AC、BD相交于點(diǎn)O，由性質(zhì)2有AO=BO=CO=DO=AC=BD．因此可以得到直角三角形的一個(gè)性質(zhì)：（ ） 四、例習(xí)題分析 例1 （教材P104例1）已知：如圖，矩形ABCD的兩條對(duì)角線相交于點(diǎn)O，∠AOB=60°，AB=4cm，求矩形對(duì)角線的長(zhǎng)． 例2（補(bǔ)充）已知：如圖 ，矩形 ABCD，AB長(zhǎng)8 cm ，對(duì)角線比AD邊長(zhǎng)4 cm．求AD的長(zhǎng)及點(diǎn)A到BD的距離AE的長(zhǎng)． 例3（補(bǔ)充） 已知：如圖，矩形ABCD中，E

4、是BC上一點(diǎn)，DF⊥AE于F，若AE=BC． 求證：CE＝EF． 五、隨堂練習(xí) 1．（填空） （1）矩形的定義中有兩個(gè)條件：一是 ，二是 ． （2）已知矩形的一條對(duì)角線與一邊的夾角為30°，則矩形兩條對(duì)角線相交所得的四個(gè)角的度數(shù)分別為 、 、 、 ． （3）已知矩形的一條對(duì)角線長(zhǎng)為10cm，兩條對(duì)角線的一個(gè)交角為120°，則矩形的邊長(zhǎng)分別為 cm， cm， cm， cm． 2．（選擇） （1）下列說(shuō)法錯(cuò)

5、誤的是（ ）． （A）矩形的對(duì)角線互相平分 （B）矩形的對(duì)角線相等 （C）有一個(gè)角是直角的四邊形是矩形 （D）有一個(gè)角是直角的平行四邊形叫做矩形 （2）矩形的對(duì)角線把矩形分成的三角形中全等三角形一共有（ ）． （A）2對(duì) （B）4對(duì) （C）6對(duì) （D）8對(duì) 3．已知：如圖，O是矩形ABCD對(duì)角線的交點(diǎn)，AE平分∠BAD，∠AOD=120°，求∠AEO的度數(shù)． 六、課后練習(xí) 1．（選擇）矩形的兩條對(duì)角線的夾角為60°，對(duì)角線長(zhǎng)為15cm，較短邊的長(zhǎng)為（ ）． (A)12cm (B)10cm (C)7.5cm (D)5cm 2．在直角三角形ABC中，∠C=90°，AB=2AC，求∠A、∠B的度數(shù)． 3．已知：矩形ABCD中，BC=2AB，E是BC的中點(diǎn)，求證：EA⊥ED． 4．如圖，矩形ABCD中，AB=2BC，且AB=AE，求證：∠CBE的度數(shù)．