《2021版中考數(shù)學(xué)精練精析 第三十六課時(shí) 相似三角形知能綜合檢測(cè) 北師大版》由會(huì)員分享，可在線閱讀，更多相關(guān)《2021版中考數(shù)學(xué)精練精析 第三十六課時(shí) 相似三角形知能綜合檢測(cè) 北師大版（7頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

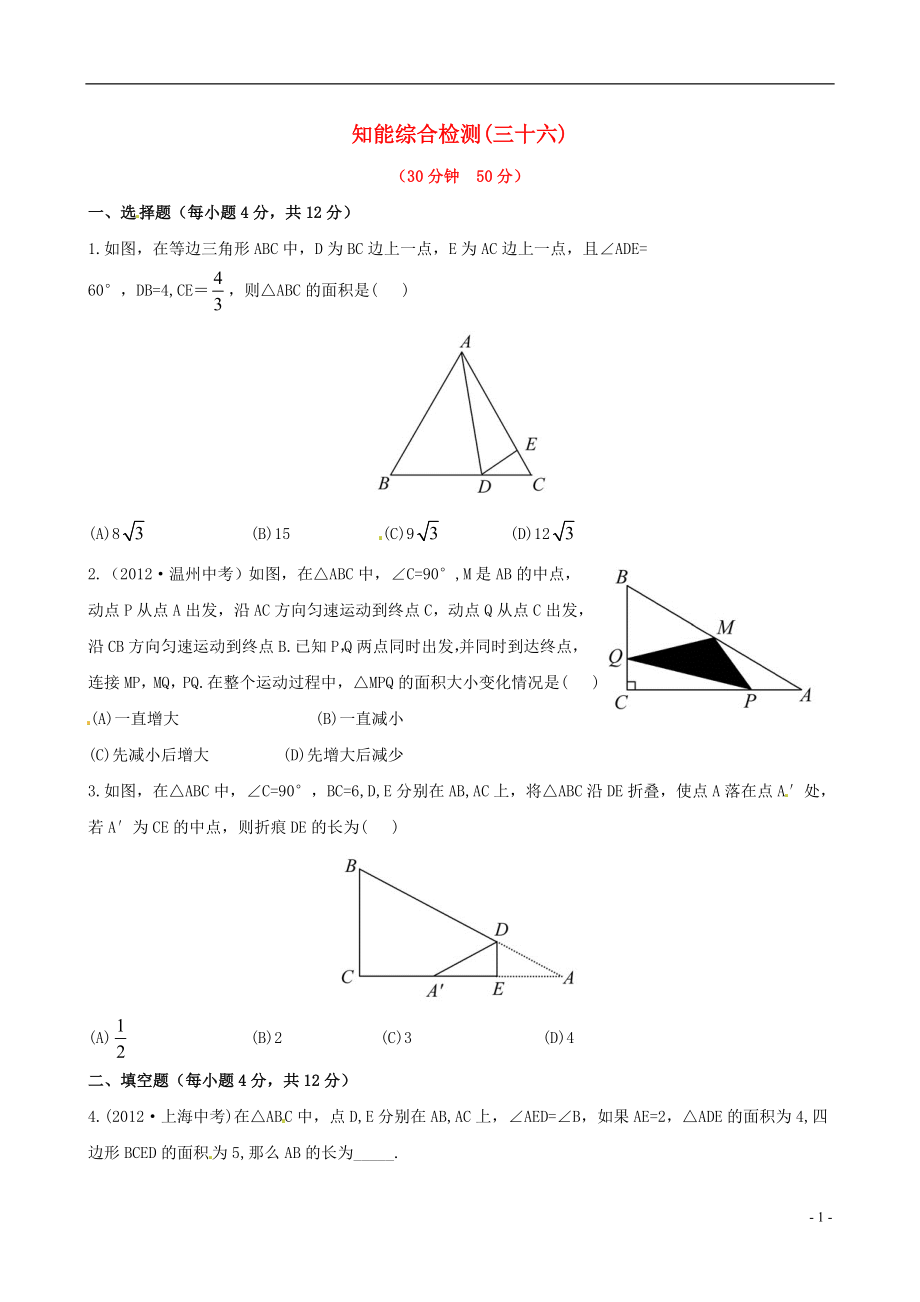
1、 知能綜合檢測(cè)(三十六) （30分鐘 50分） 一、選擇題（每小題4分，共12分） 1.如圖，在等邊三角形ABC中，D為BC邊上一點(diǎn)，E為AC邊上一點(diǎn)，且∠ADE= 60°，DB=4,CE＝，則△ABC的面積是( ) (A)8 (B)15 (C)9 (D)12 2.（2012·溫州中考）如圖，在△ABC中，∠C=90°,M是AB的中點(diǎn)，動(dòng)點(diǎn)P從點(diǎn)A出發(fā)，沿AC方向勻速運(yùn)動(dòng)到終點(diǎn)C，動(dòng)點(diǎn)Q從點(diǎn)C出發(fā)，沿CB方向勻速運(yùn)動(dòng)到終點(diǎn)B.已知P，Q兩點(diǎn)同時(shí)出發(fā)，并同時(shí)到達(dá)終點(diǎn)，連接MP，MQ，PQ.在整個(gè)運(yùn)動(dòng)過程中，△MPQ的面積大小變化情況是( ) (A)一直

2、增大 (B)一直減小 (C)先減小后增大 (D)先增大后減少 3.如圖，在△ABC中，∠C=90°，BC=6,D,E分別在AB,AC上，將△ABC沿DE折疊，使點(diǎn)A落在點(diǎn)A′處，若A′為CE的中點(diǎn)，則折痕DE的長(zhǎng)為( ) (A) (B)2 (C)3 (D)4 二、填空題（每小題4分，共12分） 4.(2012·上海中考)在△ABC中，點(diǎn)D,E分別在AB,AC上，∠AED=∠B，如果AE=2，△ADE的面積為4,四邊形BCED的面積為5,那么AB的長(zhǎng)為_____. 5.將三角形紙片（△ABC）按如圖所示的方式折疊，使點(diǎn)B落在邊AC上，記為點(diǎn)B

3、′，折痕為EF．已知AB＝AC＝3，BC＝4，若以點(diǎn)B′,F,C為頂點(diǎn)的三角形與△ABC相似，那么BF的長(zhǎng)度是_____. 6.在△ABC中，AB=6，AC=9，點(diǎn)D在邊AB所在的直線上，且AD=2，過點(diǎn)D作DE∥BC交邊AC所在直線于點(diǎn)E，則CE的長(zhǎng)為_____． 三、解答題（共26分） 7.(8分)（2012·菏澤中考）如圖，在邊長(zhǎng)為1的小正方形組成的網(wǎng)格中，△ABC和△DEF的頂點(diǎn)都在格點(diǎn)上，P1，P2，P3，P4，P5是△DEF邊上的5個(gè)格點(diǎn)，請(qǐng)按要求完成下列各題： （1）試證明△ABC為直角三角形； （2）判斷△ABC和△DEF是否相似，并說明理由； （3）畫一個(gè)三角

4、形，它的三個(gè)頂點(diǎn)為P1,P2,P3,P4,P5中的3個(gè)格點(diǎn)并且與 △ABC相似；（要求：用尺規(guī)作圖，保留痕跡，不寫作法與證明） 8.（8分）如圖，△ABC是一張銳角三角形的硬紙片，AD是邊BC上的高，BC=40 cm，AD=30 cm，從這張硬紙片上剪下一個(gè)長(zhǎng)HG是寬HE的2倍的矩形EFGH，使它的一邊EF在BC上，頂點(diǎn)G，H分別在AC，AB上，AD與HG的交點(diǎn)為M. (1)求證：； (2)求這個(gè)矩形EFGH的周長(zhǎng). 【探究創(chuàng)新】 9.（10分）如圖，在矩形ABCD中，AB＝12 cm，BC＝6 cm，點(diǎn)P沿AB邊從A向B以2 cm/s的速度移動(dòng)；點(diǎn)Q沿DA邊從D向A以1 cm

5、/s的速度移動(dòng).如果P，Q同時(shí)出發(fā)，用t（s）表示移動(dòng)時(shí)間（0≤t≤6），那么： （1）當(dāng)t為何值時(shí)，△QAP為等腰直角三角形？ （2）求四邊形QAPC的面積，你有什么發(fā)現(xiàn)？ （3）當(dāng)t為何值時(shí)，以點(diǎn)A，P，Q為頂點(diǎn)的三角形與△ABC相似？ 答案解析 1.【解析】選C.∠ADC=∠ADE+∠EDC =∠B+∠BAD, ∵∠ADE=∠B=60°,∴∠EDC=∠BAD. 又∵∠C=∠B=60°, ∴△DCE∽△ABD, ∴DC∶AB=EC∶DB=1∶3, ∴BC=AB=3DC, ∴DB=2DC,∴DC=2,∴BC=6, ∴△ABC的面積是9. 2.【

6、解析】選C.利用特殊值法，當(dāng)點(diǎn)P和點(diǎn)Q分別在點(diǎn)A和點(diǎn)C處及當(dāng)點(diǎn)P和點(diǎn)Q分別在點(diǎn)C和點(diǎn)B處時(shí)，△MPQ的面積為△ABC的面積的一半;當(dāng)點(diǎn)P和點(diǎn)Q分別在AC和BC的中點(diǎn)時(shí)，△MPQ∽△CBA，相似比為1∶2，△MPQ的面積為 △ABC的面積的，所以△MPQ的面積先減小后增大. 3.【解析】選B.根據(jù)題意可得∠DEA=∠C=90°，∠A=∠A,所以△ACB∽△AED.因?yàn)锳′為CE的中點(diǎn)，且AE=A′E,所以.根據(jù)相似三角形的性質(zhì)可得,即，解得DE=2. 4.【解析】因?yàn)椤螦ED=∠B，∠A=∠A,所以△ADE∽△ACB，所以， 所以.又因?yàn)锳E=2,所以AB=3. 答案：3 5.【解析

7、】設(shè)BF=x,由折疊知，B′F=BF=x. ∴FC=4-x,當(dāng)△B′CF∽△ACB時(shí)， 得B′F∶AB=CF∶CB, 即x∶3=(4-x)∶4,∴3(4-x)=4x,∴x=. 當(dāng)△B′CF∽△BCA時(shí)，有∠FB′C=∠B. ∵AB=AC,∴∠B=∠C, ∴∠FB′C=∠C,∴B′F=FC=BF, 即F為BC的中點(diǎn)，∴BF=2. 答案：或2 6.【解析】如圖①，當(dāng)點(diǎn)D在邊AB上時(shí)，∵AB=6，AC=9，AD=2， ∴BD=AB-AD=6-2=4.∵DE∥BC， ∴，即，∴CE=6；如圖②，當(dāng)點(diǎn)D在BA的延長(zhǎng)線上時(shí)， ∵AB=6，AC=9，AD=2，∴,即,∴AE=3,∴C

8、E=AE+AC=12. 綜上，CE的長(zhǎng)為6或12． 答案：6或12 【歸納整合】常見的相似三角形的基本圖形 （1）A型，如圖所示： （2）共角型，如圖所示： （3）X型，如圖所示： （4）K型，如圖所示： 7.【解析】（1）根據(jù)勾股定理，得AB=2，AC=，BC=5, 顯然有AB2+AC2=BC2， 根據(jù)勾股定理的逆定理得△ABC 為直角三角形. （2）△ABC和△DEF相似． 根據(jù)勾股定理，得AB=2，AC=，BC=5, DE=4，DF=2，EF=2． ∵, ∴△ABC∽△DEF． （3）如圖：△P4P5P2． 8.【解析】(1)∵四

9、邊形EFGH為矩形，∴HG∥EF， ∴∠AHG=∠B，∠AGH=∠C，∴△AHG∽△ABC， 又∵AD是邊BC上的高，∴AD⊥BC，AM⊥HG， ∴ (2)設(shè)HE=x cm，則MD=x cm，HG=2x cm， 由（1）知， 因?yàn)锽C=40 cm，AD=30 cm， 所以，解得x=12. 則HG=2x=24，所以矩形EFGH的周長(zhǎng)為 2（HE+HG）=2×（12+24）=72(cm). 9.【解析】（1）對(duì)于任意時(shí)刻的t有：AP=2t，DQ=t， AQ=6-t， 當(dāng)AQ=AP時(shí)，△QAP為等腰直角三角形, 即6-t=2t，∴t=2， ∴當(dāng)t=2時(shí)，△QAP為等腰直

10、角三角形. （2）在△AQC中，AQ=6-t，AQ邊上的高CD=12， ∴S△AQC=(6-t)×12=36-6t; 在△APC中，AP=2t，AP邊上的高CB=6， ∴S△APC=×2t×6=6t. ∴四邊形QAPC的面積 S四邊形QAPC=S△AQC+S△APC=36-6t+6t=36（cm2）, 所以，經(jīng)計(jì)算發(fā)現(xiàn)：點(diǎn)P，Q在運(yùn)動(dòng)的過程中，四邊形QAPC的面積保持不變. （3）根據(jù)題意，應(yīng)分兩種情況來研究： ①當(dāng)時(shí)，△QAP∽△ABC， 則有，求得t=1.2（秒）. ②當(dāng)時(shí)，△PAQ∽△ABC， 則有，求得t=3（秒） . ∴當(dāng)t=1.2或3秒時(shí)，以點(diǎn)A，P，Q為頂點(diǎn)的三角形與△ABC相似. - 7 -