《高中數(shù)學學考復習 模塊過關專題講座練習 第七講 直線與平面垂直的判定與性質 新人教A版必修2》由會員分享，可在線閱讀，更多相關《高中數(shù)學學考復習 模塊過關專題講座練習 第七講 直線與平面垂直的判定與性質 新人教A版必修2（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

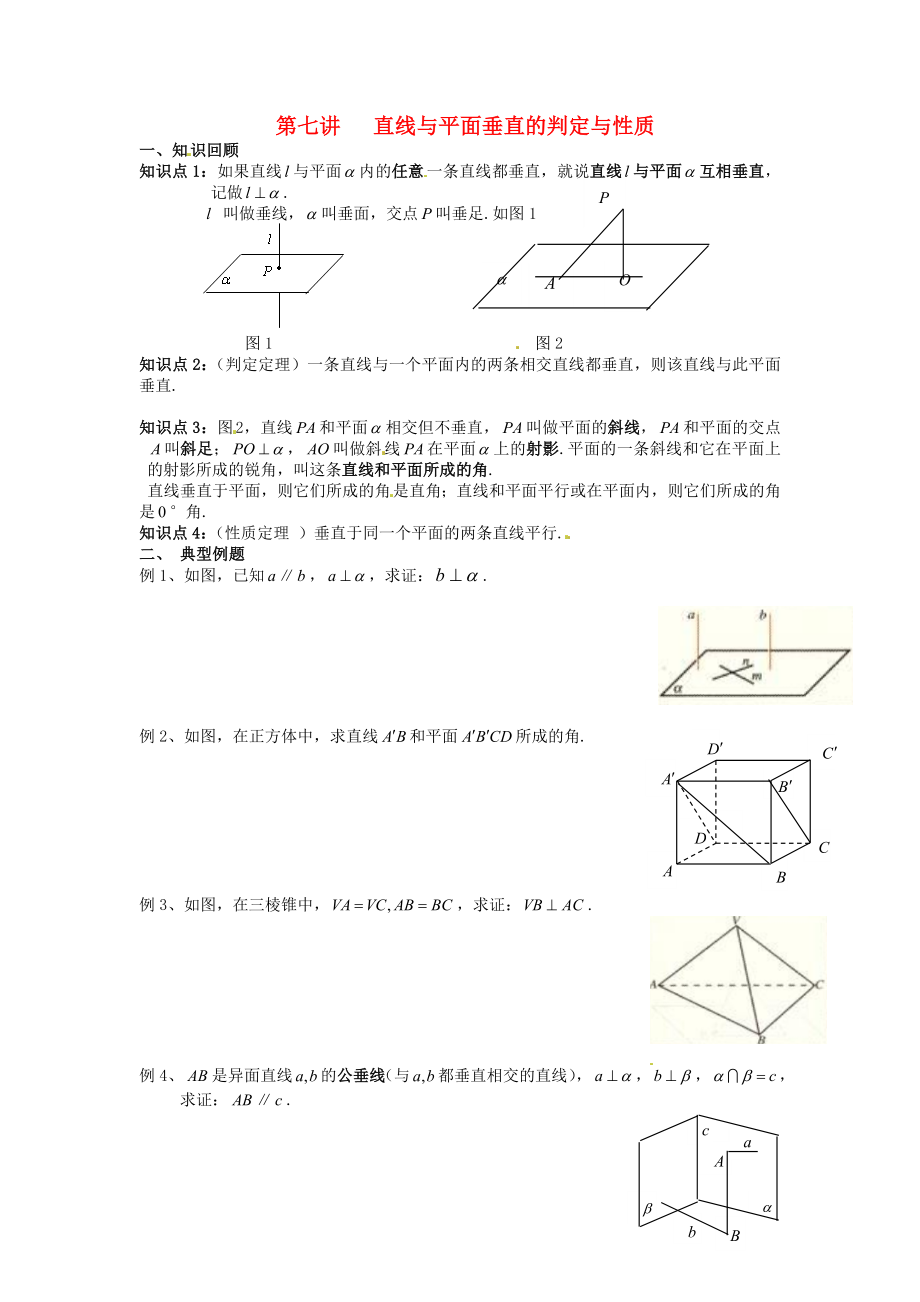
1、第七講 直線與平面垂直的判定與性質 一、知識回顧 知識點1：如果直線與平面內(nèi)的任意一條直線都垂直，就說直線與平面互相垂直，記做. 叫做垂線，叫垂面，交點叫垂足.如圖1 圖1 圖2 知識點2：（判定定理）一條直線與一個平面內(nèi)的兩條相交直線都垂直，則該直線與此平面垂直. 知識點3：圖2，直線和平面相交但不垂直，叫做平面的斜線，和平面的交點叫斜足；，叫做斜線在平面上的射影.平面的一條斜線和它在平面上的射影所成的銳角，叫這條直線和平面所成的角. 直線垂直于平面，則它們所成的角是直角；直線和平面平行

2、或在平面內(nèi)，則它們所成的角是°角. 知識點4：（性質定理 ）垂直于同一個平面的兩條直線平行. 二、 典型例題 例1、如圖，已知∥，，求證：. 例2、如圖，在正方體中，求直線和平面所成的角. 例3、如圖，在三棱錐中，，求證：. 例4、是異面直線的公垂線（與都垂直相交的直線），，，， 求證：∥. 三、課堂練習 1. 已知直線和平面，下列錯誤的是（ ）. A. B. C.∥或 D.∥ 2. 下列四個命題中錯誤的

3、是（ ）. A.∥ B.∥ C.∥ D.∥ 3. ，且∥，則直線和面是（ ）. A. B.與相交或∥或 C. D.∥或 4. 過平面外一點：①存在無數(shù)條直線與平面平行②存在無數(shù)條直線與平面垂直 ③僅有一條直線與平面平行④僅有一條直線與平面垂直；其中正確結論的個數(shù)是（ ）. A.1個 B.2個 C.3個 D.4個 5.若平面∥平面,直線,則與_____. 6.在三棱錐中，，，若是的中點，試確定上點的位置，使得. 四、總結提升 1. 直線與平面垂直的定義、判定、性質；線線垂直與線面

4、垂直的轉化； 2. 直線與平面所成的角的定義及求法. 3. “平行”與“垂直”關系的相互轉化. ※ 知識拓展 求直線與平面所成的角關鍵是作出斜線上一點到平面的垂線，找到這點的射影—垂足的位置.確定點的射影位置的方法有①斜線上任意一點在平面上的射影必在斜線在平面內(nèi)的射影上②一個點到一個角的兩邊距離相等，則這個點的射影在這個角的角平分線上③若兩個面垂直，則一個面上的點在另一面上的射影必在兩個平面的交線上. 五、課后作業(yè) 1. 如圖，在正方體中，是底面的中心，，為垂足，求證：面. 2. 如圖，，，， ，求證：，.