《2014-2015學(xué)年高中數(shù)學(xué)（蘇教版必修二） 第一章立體幾何初步 第1章 章末總結(jié) 課時(shí)作業(yè)（含答案）》由會(huì)員分享，可在線閱讀，更多相關(guān)《2014-2015學(xué)年高中數(shù)學(xué)（蘇教版必修二） 第一章立體幾何初步 第1章 章末總結(jié) 課時(shí)作業(yè)（含答案）（7頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

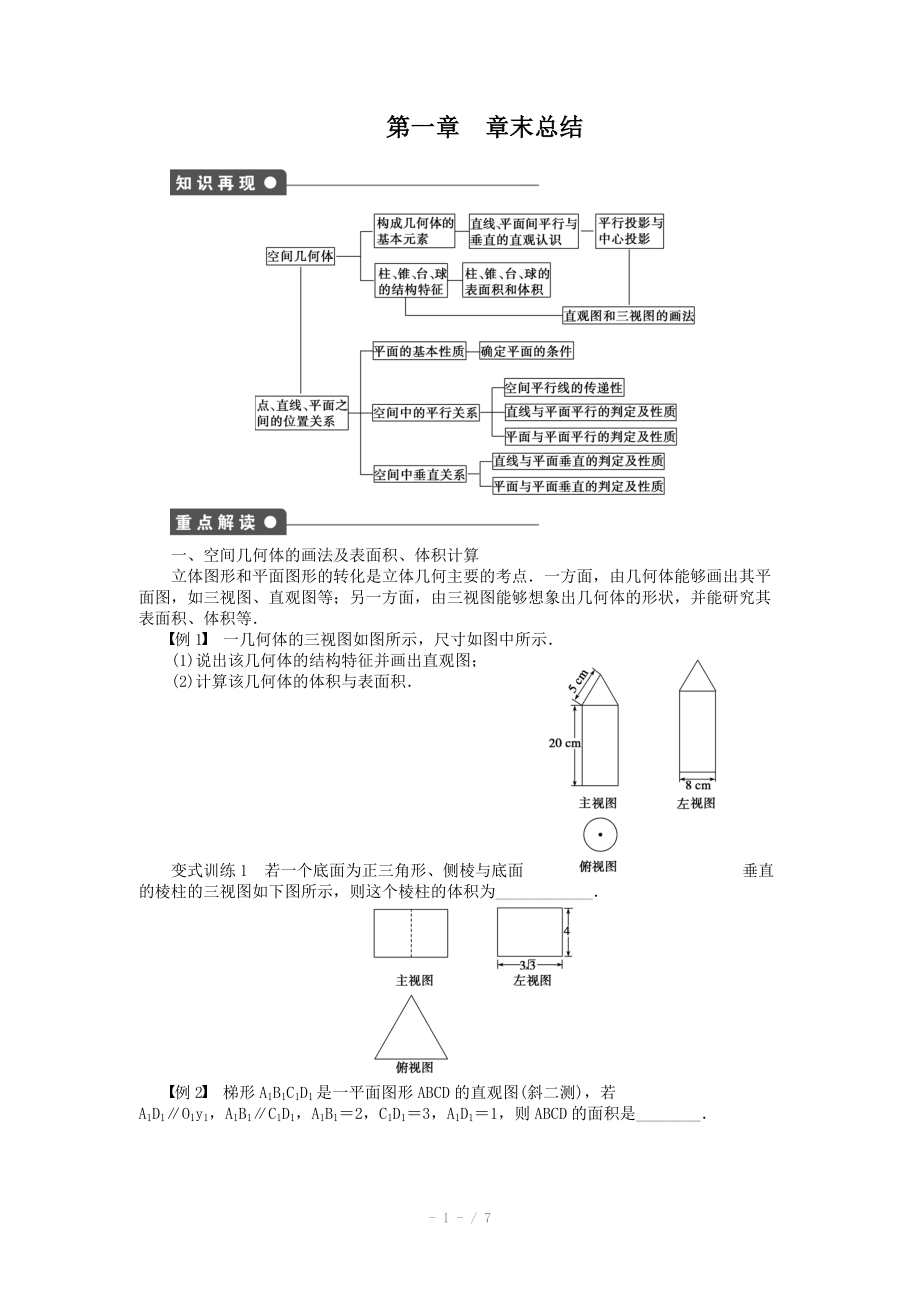
1、 第一章 章末總結(jié) 一、空間幾何體的畫法及表面積、體積計(jì)算 立體圖形和平面圖形的轉(zhuǎn)化是立體幾何主要的考點(diǎn)．一方面，由幾何體能夠畫出其平面圖，如三視圖、直觀圖等；另一方面，由三視圖能夠想象出幾何體的形狀，并能研究其表面積、體積等． 例1　一幾何體的三視圖如圖所示，尺寸如圖中所示． (1)說(shuō)出該幾何體的結(jié)構(gòu)特征并畫出直觀圖； (2)計(jì)算該幾何體的體積與表面積． 變式訓(xùn)練1　若一個(gè)底面為正三角形、側(cè)棱與底面垂直的棱柱的三視圖如下圖所示，則這個(gè)棱柱的體積為____________． 例2　梯形A1B1C1D1是一平面圖形A

2、BCD的直觀圖(斜二測(cè))，若A1D1∥O1y1，A1B1∥C1D1，A1B1＝2，C1D1＝3，A1D1＝1，則ABCD的面積是________． - 1 - / 7 變式訓(xùn)練2　等腰梯形ABCD，上底CD＝1，腰AD＝CB＝，下底AB＝3，以下底所在直線為x軸，則由斜二測(cè)畫法畫出的直觀圖A′B′C′D′的面積為______． 二、平面基本性質(zhì)的應(yīng)用 1．關(guān)于多點(diǎn)共線問題往往需證明這些點(diǎn)在某兩個(gè)平面的交線上． 2．多線共點(diǎn)問題的證明往往讓其他線都過某兩條線的交點(diǎn)． 3．多點(diǎn)共面問題的證明往往讓其他點(diǎn)在某三點(diǎn)或四點(diǎn)確定的平面上． 4．多線共面問題的證明往往讓其他線在某兩條直

3、線確定的平面內(nèi)． 例3　如圖所示，空間四邊形ABCD中，E，F(xiàn)分別為AB，AD的中點(diǎn)，G，H分別在BC，CD上，且BG∶GC＝DH∶HC＝1∶2． 求證：(1)E、F、G、H四點(diǎn)共面； (2)GE與HF的交點(diǎn)在直線AC上． 變式訓(xùn)練3　如圖，四邊形ABB′A′，BCC′B′，CAA′C′都是梯形．求證：三直線AA′，BB′，CC′相交于一點(diǎn)． 三、直線、平面的位置關(guān)系 1．空間平行關(guān)系的判定方法： (1)判定線線平行的方法． ①利用線線平行的定義證共面而且無(wú)公共點(diǎn)(結(jié)合反證法)； ②利用平行公理4

4、； ③利用線面平行性質(zhì)定理； ④利用線面垂直的性質(zhì)定理(若a⊥α，b⊥α，則a∥b)； ⑤利用面面平行性質(zhì)定理(若α∥β，α∩γ＝a，β∩γ＝b，則a∥b)． (2)判斷線面平行的方法： ①線面平行的定義(無(wú)公共點(diǎn))； ②利用線面平行的判定定理(a?α，b?α，a∥b?a∥α)； ③面面平行的性質(zhì)定理(α∥β，a?α?a∥β)； ④面面平行的性質(zhì)(α∥β，a?α，a?β，a∥α?a∥β)． (3)面面平行的判定方法有： ①平面平行的定義(無(wú)公共點(diǎn))； ②判定定理(若a∥β，b∥β，a、b?α，且a∩b＝A，則α∥β)； ③判定定理的推論(若a∥a′，b∥b′，a

5、?α，b?α且a∩b＝A，a′?β，b′?β，且a′∩b′＝A′，則α∥β)； ④線面垂直性質(zhì)定理(若a⊥α，a⊥β，則α∥β)； ⑤平面平行的性質(zhì)(傳遞性：α∥β，β∥γ?α∥γ)． 平行關(guān)系的轉(zhuǎn)化是： 2．空間垂直關(guān)系的判定方法： (1)判定線線垂直的方法有： ①計(jì)算所成的角為90(包括平面角和異面直線所成的角)； ②線面垂直的性質(zhì)(若a⊥α，b?α，則a⊥b)； ③面面垂直的定義：若兩平面垂直，則兩平面相交形成的二面角的平面角為90． (2)判定線面垂直的方法有： ①線面垂直定義(一般不易驗(yàn)證任意性)； ②線面垂直的判定定理(a⊥b，a⊥c，b?α，c?α，b∩

6、c＝M?a⊥α)； ③平行線垂直平面的傳遞性質(zhì)(a∥b，b⊥α?a⊥α)； ④面面垂直的性質(zhì)(α⊥β，α∩β＝l，a?β，a⊥l?a⊥α)； ⑤面面平行的性質(zhì)(a⊥α，α∥β?a⊥β)； ⑥面面垂直的性質(zhì)(α∩β＝l，α⊥γ，β⊥γ?l⊥γ)． (3)面面垂直的判定方法有： ①根據(jù)定義(作兩平面構(gòu)成二面角的平面角，計(jì)算其為90)； ②面面垂直的判定定理(a⊥β，a?α?α⊥β)． 垂直關(guān)系的轉(zhuǎn)化是： 例4　如圖所示，在四棱錐P—ABCD中，側(cè)面PAD是正三角形，且與底面ABCD垂直，底面ABCD是邊長(zhǎng)為2的菱形，∠BAD＝60，N是PB的中點(diǎn)，過A，D，N的平面交PC于M

7、，E為AD的中點(diǎn)．求證： (1)EN∥平面PDC； (2)BC⊥平面PEB； (3)平面PBC⊥平面ADMN． 變式訓(xùn)練4　如圖所示，在四棱錐P—ABCD中，底面ABCD是正方形，側(cè)棱PD⊥底面ABCD，PD＝DC，E是PC的中點(diǎn)，過E點(diǎn)作EF⊥PB交PB于點(diǎn)F．求證： (1)PA∥平面EDB； (2)PB⊥平面EFD． 第一章 章末總結(jié) 答案 例1　 解　(1)由三視圖知該幾何體是由一個(gè)圓柱與一個(gè)等底圓錐拼接而成的組合體，其直觀圖如圖所示． (2)由三視圖中尺寸知，組合體下

8、部是底面直徑為8 cm，高為20 cm的圓柱，上部為底面直徑為8 cm，母線長(zhǎng)為5 cm的圓錐． 易求得圓錐高h(yuǎn)＝＝3(cm)， ∴體積V＝π4220＋π423＝336π(cm3)， 表面積S＝π42＋2π420＋π45 ＝196π(cm2)． ∴該幾何體的體積為336π cm3，表面積為196π cm2． 點(diǎn)評(píng)　三視圖畫法：它包括主視圖、左視圖、俯視圖三種．畫圖時(shí)要遵循“高平齊、長(zhǎng)對(duì)正、寬相等”的原則，同時(shí)還要注意被擋住的輪廓線畫成虛線． 變式訓(xùn)練1　36 解析　觀察三視圖得棱柱底面正三角形的高和側(cè)棱長(zhǎng)．注意圖中數(shù)據(jù)3是底面正三角形的高，不是邊長(zhǎng)． 棱柱的側(cè)棱長(zhǎng)為4，底面正

9、三角形的高為3，設(shè)邊長(zhǎng)為a，則a＝3，所以a＝6．所以底面積為a2＝9．所以棱柱的體積為94＝36． 例2　5 解析　把圖還原，ABCD為直角梯形，AB＝A1B1＝2，CD＝C1D1＝3，AD＝2A1D1＝2． ∴S梯ABCD＝＝5． 點(diǎn)評(píng)　斜二測(cè)畫法：主要用于水平放置的平面圖畫法或立體圖形的畫法．它的主要步驟：①畫軸；②畫平行于x，y，z軸的線段分別為平行于x′，y′，z′軸的線段；③截線段，平行于x，z軸的線段的長(zhǎng)度不變，平行于y軸的線段的長(zhǎng)度變?yōu)樵瓉?lái)的一半． 變式訓(xùn)練2　 解析　 ∵OE＝＝1，∴O′E′＝，E′F＝， ∴直觀圖A′B′C′D′的面積為

10、S′＝(1＋3)＝． 例3　證明　(1)∵BG∶GC＝DH∶HC， ∴GH∥BD，又EF∥BD，∴EF∥GH， ∴E、F、G、H四點(diǎn)共面． (2)∵G，H不是BC、CD的中點(diǎn)，∴EF≠GH． 又EF∥GH， ∴EG與FH不平行，則必相交，設(shè)交點(diǎn)為M． ?M∈面ABC且M∈面ACD ?M在面ABC與面ACD的交線上 ?M∈AC． ∴GE與HF的交點(diǎn)在直線AC上． 點(diǎn)評(píng)　證明線共點(diǎn)、點(diǎn)共線、線共面問題，重要是應(yīng)用平面的基本性質(zhì)，先證部分元素共點(diǎn)、共線、共面，再利用公理1,2,3證明其他元素也具有這個(gè)性質(zhì)，要熟練地掌握這三個(gè)公理． 變式訓(xùn)練3　證明　梯形ABB′A′中，A′B

11、′∥AB． ∴AA′，BB′在同一平面A′B內(nèi)． 設(shè)直線AA′，BB′相交于點(diǎn)P， 同理BB′、CC′同在平面BC′內(nèi)，CC′、AA′同在平面A′C內(nèi)． ∵P∈AA′，AA′?平面A′C， ∴P∈平面A′C． 同理點(diǎn)P∈平面BC′． 根據(jù)公理2，點(diǎn)P在平面A′C與平面BC′的交線上，而平面A′C∩平面BC′＝CC′，故點(diǎn)P ∈直線CC′，即三直線AA′、BB′、CC′相交于一點(diǎn)． 例4　證明　(1)因?yàn)锳D∥BC，BC?平面PBC， AD?平面PBC，所以AD∥平面PBC， 又平面ADMN∩平面PBC＝MN， 所以AD∥MN，所以MN∥BC． 因?yàn)镹為PB的

12、中點(diǎn)，所以M為PC的中點(diǎn)， 所以MN∥BC，且MN＝BC． 又E為AD的中點(diǎn)， 所以四邊形DENM為平行四邊形． 所以EN∥DM． 又EN?平面PDC，DM?平面PDC， 所以EN∥平面PDC． (2)因?yàn)锳BCD為邊長(zhǎng)為2的菱形，且∠BAD＝60， 所以BE⊥AD．又因?yàn)镻E⊥AD，PE∩BE＝E， 所以AD⊥平面PEB． 因?yàn)锳D∥BC，所以BC⊥平面PEB． (3)由(2)知AD⊥PB． 又因?yàn)镻A＝AB且N為PB的中點(diǎn)， 所以AN⊥PB，又AD∩AN＝A， 所以PB⊥平面ADMN． 又PB?平面PBC，所以平面PBC⊥平面ADMN． 點(diǎn)評(píng)　立體幾何的證明

13、，我們要牢牢抓住“轉(zhuǎn)化”這一思想，線與線，線與面，面與面之間的垂直與平行都可互相轉(zhuǎn)化，轉(zhuǎn)化的理論依據(jù)是這三種平行與垂直的判定定理、性質(zhì)定理等． 變式訓(xùn)練4　證明　(1)如圖所示，連結(jié)AC交BD于O，連結(jié)EO． ∵底面ABCD是正方形， ∴點(diǎn)O是AC的中點(diǎn)． 在△PAC中，EO是中位線， ∴PA∥EO． 而EO?平面EDB且PA?平面EDB， ∴PA∥平面EDB． (2)∵PD⊥底面ABCD，且DC?平面ABCD， ∴PD⊥DC．∵PD＝DC， ∴△PDC是等腰直角三角形． 又DE是斜邊PC的中線，∴DE⊥PC． ① 由PD⊥底面ABCD，得PD⊥BC． ∵底面ABCD是正方形，∴DC⊥BC． ∴BC⊥平面PDC． 又DE?平面PDC，∴BC⊥DE． ② 由①和②推得DE⊥平面PBC． 而PB?平面PBC，∴DE⊥PB． 又EF⊥PB，且DE∩EF＝E， ∴PB⊥平面EFD． 希望對(duì)大家有所幫助，多謝您的瀏覽！