《人教版八年級數(shù)學(xué)上冊第十二章全等三角形復(fù)習(xí)課導(dǎo)學(xué)案無答案》由會員分享，可在線閱讀，更多相關(guān)《人教版八年級數(shù)學(xué)上冊第十二章全等三角形復(fù)習(xí)課導(dǎo)學(xué)案無答案（2頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、第十一章全等三角形復(fù)習(xí)（1、2） 一、歸納總結(jié)，完善認知 1.總結(jié)本章知識點及相互聯(lián)系.兩兩邊一____ 兩邊一對角 ____________ ____________ 三邊______________ ___邊_____________ 兩角一邊對應(yīng)相等 __________________ 一個條件 兩個條件 三個條件 2.三角形全等 探究 三角形 全等的 條件 二、基本訓(xùn)練，掌握雙基 1.填空 (1)能夠 的兩個圖形叫做全等形，能夠 的兩個三角形叫做全等三角形.

2、 (2)把兩個全等的三角形重合到一起，重合的頂點叫做 ，重合的邊叫做 ，重合的角叫做 . (3)全等三角形的 邊相等，全等三角形的 角相等. (4) 對應(yīng)相等的兩個三角形全等（邊邊邊或 ）. (5)兩邊和它們的 對應(yīng)相等的兩個三角形全等（邊角邊或 ）. (6)兩角和它們的 對應(yīng)相等的兩個三角形全等（角邊角或 ）. (7)兩角和其中一角的 對

3、應(yīng)相等的兩個三角形全等（角角邊或 ）. (8) 和一條 對應(yīng)相等的兩個直角三角形全等（斜邊、直角邊或 ）. (9)角的 上的點到角的兩邊的距離相等. 2.如圖，圖中有兩對三角形全等，填空： (1)△CDO≌ ，其中，CD的對應(yīng)邊是 ， DO的對應(yīng)邊是 ，OC的對應(yīng)邊是 ； (2)△ABC≌ ，∠A的對應(yīng)角是 ， ∠B的對應(yīng)角是 ，∠ACB的對應(yīng)角是 .

4、3.判斷對錯：對的畫“√”，錯的畫“”. (1)一邊一角對應(yīng)相等的兩個三角形不一定全等. （ ） (2)三角對應(yīng)相等的兩個三角形一定全等. （ ） (3)兩邊一角對應(yīng)相等的兩個三角形一定全等. （ ） (4)兩角一邊對應(yīng)相等的兩個三角形一定全等. （ ） (5)三邊對應(yīng)相等的兩個三角形一定全等. （ ） (6)兩直角邊對應(yīng)相等的兩個直角三角形一定全等.

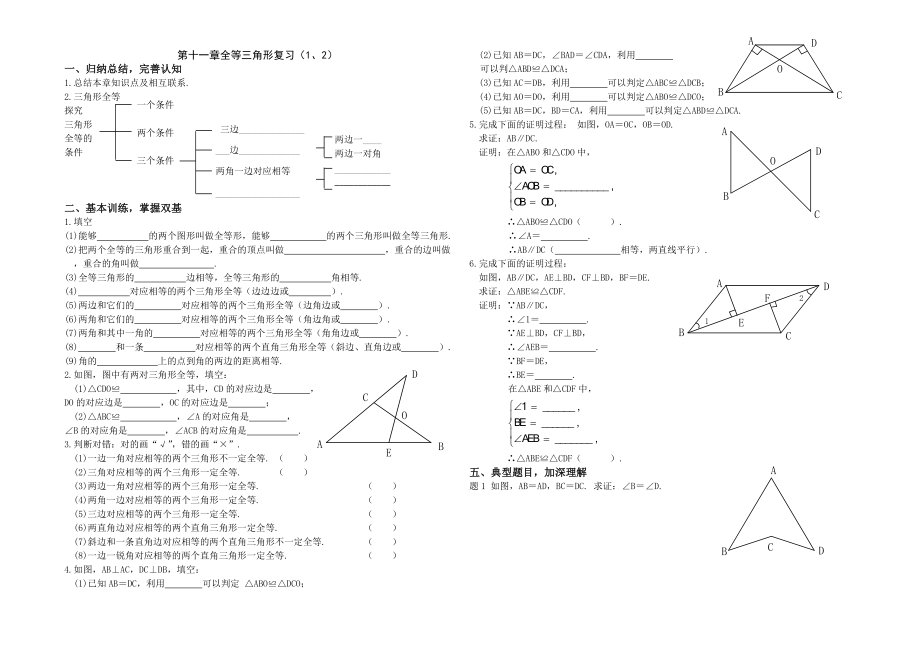
5、 （ ） (7)斜邊和一條直角邊對應(yīng)相等的兩個直角三角形不一定全等. （ ） (8)一邊一銳角對應(yīng)相等的兩個直角三角形一定全等. （ ） 4.如圖，AB⊥AC，DC⊥DB，填空： (1)已知AB＝DC，利用 可以判定 △ABO≌△DCO； (2)已知AB＝DC，∠BAD＝∠CDA，利用 可以判△ABD≌△DCA； (3)已知AC＝DB，利用 可以判定△ABC≌△DCB； (4)已知AO＝DO，利用 可以判定△ABO≌△DCO； (

6、5)已知AB＝DC，BD＝CA，利用 可以判定△ABD≌△DCA. 5.完成下面的證明過程： 如圖，OA＝OC，OB＝OD. 求證：AB∥DC. 證明：在△ABO和△CDO中， ∴△ABO≌△CDO（ ）. ∴∠A＝ . ∴AB∥DC（ 相等，兩直線平行）. 6.完成下面的證明過程： 如圖，AB∥DC，AE⊥BD，CF⊥BD，BF＝DE. 求證：△ABE≌△CDF. 證明：∵AB∥DC， ∴∠1＝ .

7、 ∵AE⊥BD，CF⊥BD， ∴∠AEB＝ . ∵BF＝DE， ∴BE＝ . 在△ABE和△CDF中， ∴△ABE≌△CDF（ ）. 五、典型題目，加深理解 題1 如圖，AB＝AD，BC＝DC. 求證：∠B＝∠D. 題2 證明：角的內(nèi)部到角的兩邊的距離相等的點在角的平分線上. 題3 如圖，CD⊥AB，BE⊥AC，OB＝OC.求證：∠1＝∠2.

8、 六、綜合運用，發(fā)展能力 7.如圖，OA⊥AC，OB⊥BC，填空： (1)利用“角的平分線上的點到角的兩邊 的距離相等”，已知 ＝ ， 可得 ＝ ； (2)利用“角的內(nèi)部到角兩邊距離相等的點在角的平分線上”， 已知 ＝ ，可得 ＝ . 8.如圖，要在S區(qū)建一個集貿(mào)市場， 使它到公路、鐵路的距離相等，并且離公路與鐵路交叉處300米.如果圖中1厘米表示100米，請在圖中標出集貿(mào)市場的位置. 9.如圖，CD＝CA，∠1＝∠2，EC＝BC.求證：DE

9、＝AB. 10.如圖，AB＝DE，AC＝DF，BE＝CF.求證：AB∥DE. 11.如圖，在△ABC中，D是BC的中點， DE⊥AB，DF⊥AC，BE＝CF. 求證：AD是△ABC的角平分線. 12.如圖，∠ACB=90,AC=BC，BE⊥CE，AD⊥CE. 求證：△ACD≌△CBE.