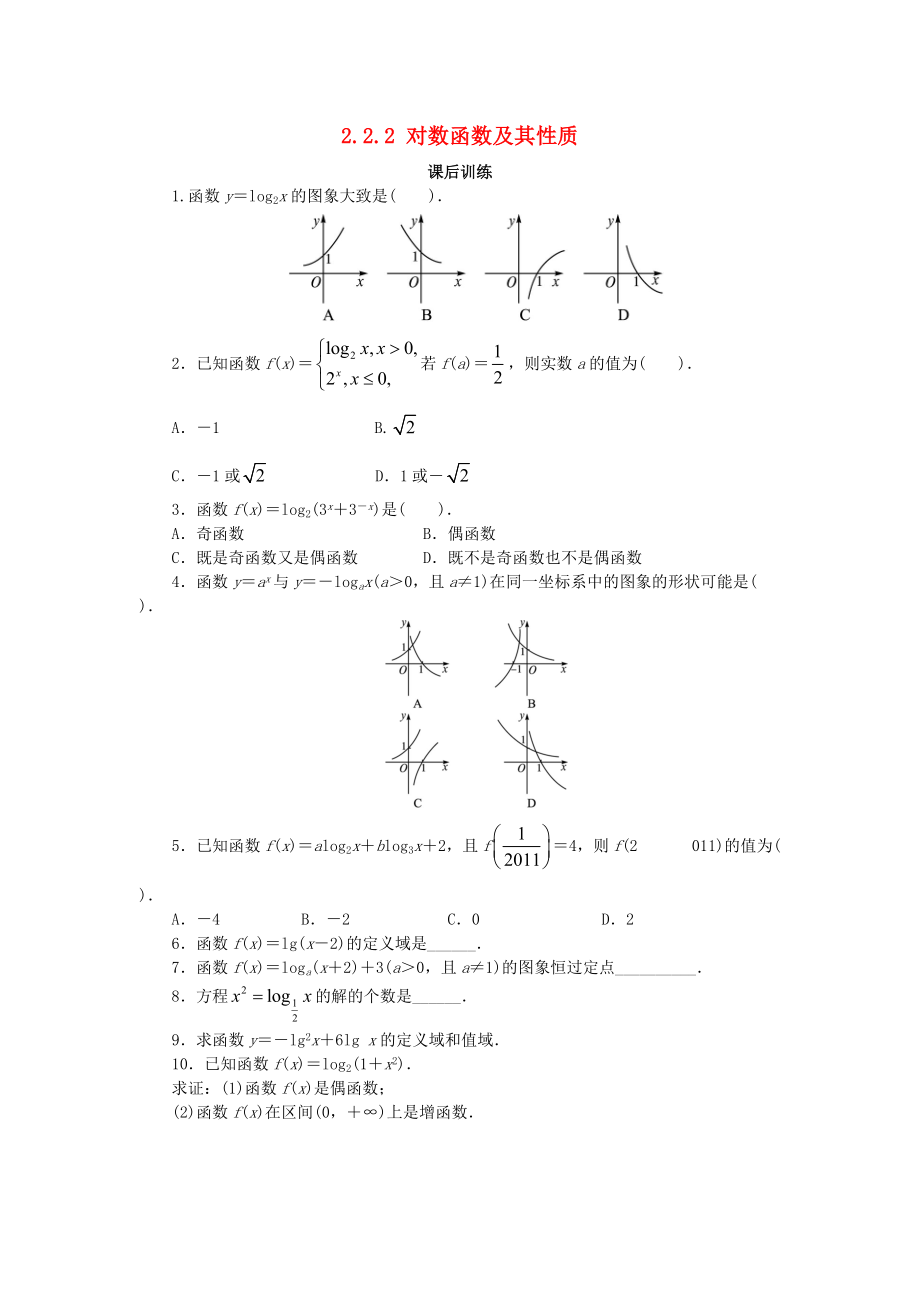
《高中數(shù)學(xué) 第二章 基本初等函數(shù)Ⅰ2.2 對(duì)數(shù)函數(shù) 2.2.2 對(duì)數(shù)函數(shù)及其性質(zhì)1課后訓(xùn)練1 新人教A版必修1》由會(huì)員分享，可在線閱讀，更多相關(guān)《高中數(shù)學(xué) 第二章 基本初等函數(shù)Ⅰ2.2 對(duì)數(shù)函數(shù) 2.2.2 對(duì)數(shù)函數(shù)及其性質(zhì)1課后訓(xùn)練1 新人教A版必修1（3頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

1、 2.2.2 對(duì)數(shù)函數(shù)及其性質(zhì) 課后訓(xùn)練 1.函數(shù)y＝log2x的圖象大致是(　　)． 2．已知函數(shù)f(x)＝若f(a)＝，則實(shí)數(shù)a的值為(　　)． A．－1 B. C．－1或 D．1或－ 3．函數(shù)f(x)＝log2(3x＋3－x)是(　　)． A．奇函數(shù) B．偶函數(shù) C．既是奇函數(shù)又是偶函數(shù) D．既不是奇函數(shù)也不是偶函數(shù) 4．函數(shù)y＝ax與y＝－logax(a＞0，且a≠1)在同一坐標(biāo)系中的圖象的形狀可能是(　　)． 5．已知函數(shù)f(x)＝alog

2、2x＋blog3x＋2，且f＝4，則f(2 011)的值為(　　)． A．－4 B．－2 C．0 D．2 6．函數(shù)f(x)＝lg(x－2)的定義域是______． 7．函數(shù)f(x)＝loga(x＋2)＋3(a＞0，且a≠1)的圖象恒過定點(diǎn)__________． 8．方程的解的個(gè)數(shù)是______． 9．求函數(shù)y＝－lg2x＋6lg x的定義域和值域． 10．已知函數(shù)f(x)＝log2(1＋x2)． 求證：(1)函數(shù)f(x)是偶函數(shù)； (2)函數(shù)f(x)在區(qū)間(0，＋∞)上是增函數(shù)．  參考答案 1. 答案

3、：C 2. 答案：C　當(dāng)a＞0時(shí)，log2a＝，則＝； 當(dāng)a≤0時(shí)，2a＝，即2a＝2－1，則a＝－1. 綜上，a＝－1或. 3. 答案：B　∵定義域?yàn)镽，f(－x)＝log2[3－x＋3－(－x)]＝log2(3－x＋3x)＝f(x)，∴f(x)是偶函數(shù)． 4. 答案：A　函數(shù)y＝－logax恒過定點(diǎn)(1,0)，故排除B項(xiàng)；當(dāng)a＞1時(shí)，y＝ax是增函數(shù)，y＝－logax是減函數(shù)，當(dāng)0＜a＜1時(shí)，y＝ax是減函數(shù)，y＝－logax是增函數(shù)，故排除C項(xiàng)和D項(xiàng)；A項(xiàng)正確． 5. 答案：C　f(x)＋＝alog2x＋blog3x＋2＋alog2＋blog3＋2＝4，∴f(2 011)＋＝

4、4， 又＝4，∴f(2 011)＝0. 6. 答案：(2，＋)　要使函數(shù)有意義，自變量x的取值需滿足x－2＞0，即x＞2. 7. 答案：(－1,3)　令x＋2＝1，解得x＝－1.又∵f(－1)＝3， ∴f(x)的圖象恒過定點(diǎn)(－1,3)． 8. 答案：1　在同一平面直角坐標(biāo)系中畫出函數(shù)y＝x2和函數(shù)的圖象，如圖所示，則函數(shù)y＝x2和函數(shù)的圖象僅有一個(gè)交點(diǎn)，所以方程僅有一個(gè)實(shí)數(shù)解． 9. 答案：分析：定義域可由函數(shù)的解析式直接得出，求值域可利用換元法，將其轉(zhuǎn)化為求二次函數(shù)的值域． 解：要使函數(shù)有意義，自變量x的取值需滿足x＞0， ∴函數(shù)的定義域是(0，＋)． 設(shè)lg x＝t

5、， 由于x(0，＋)，則tR， y＝－t2＋6t＝－(t－3)2＋9， ∵tR，∴y≤9. ∴函數(shù)的值域是(－，9]． 10. 答案：分析：(1)先求函數(shù)f(x)的定義域，再證明f(－x)＝f(x)；(2)依據(jù)證明函數(shù)單調(diào)性的步驟來證明即可． 證明：(1)函數(shù)f(x)的定義域是R， f(－x)＝log2[1＋(－x)2]＝log2(1＋x2)＝f(x)， 所以函數(shù)f(x)是偶函數(shù)． (2)設(shè)x1，x2為(0，＋)上的任意兩個(gè)實(shí)數(shù)，且x1＜x2，則f(x1)－f(x2)＝log2(1＋x12)－log2(1＋x22)＝log2. 由于0＜x1＜x2，則0＜x12＜x22， 則0＜1＋x12＜1＋x22， 所以0＜＜1. 又函數(shù)y＝log2x在(0，＋)上是增函數(shù)， 所以log2＜0.所以f(x1)＜f(x2)． 所以函數(shù)f(x)在區(qū)間(0，＋)上是增函數(shù)． 6EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F375