《2015屆高考數(shù)學總復習 基礎知識名師講義 第八章 第五節(jié)空間圖形的平行關系 文》由會員分享，可在線閱讀，更多相關《2015屆高考數(shù)學總復習 基礎知識名師講義 第八章 第五節(jié)空間圖形的平行關系 文（8頁珍藏版）》請在裝配圖網(wǎng)上搜索。

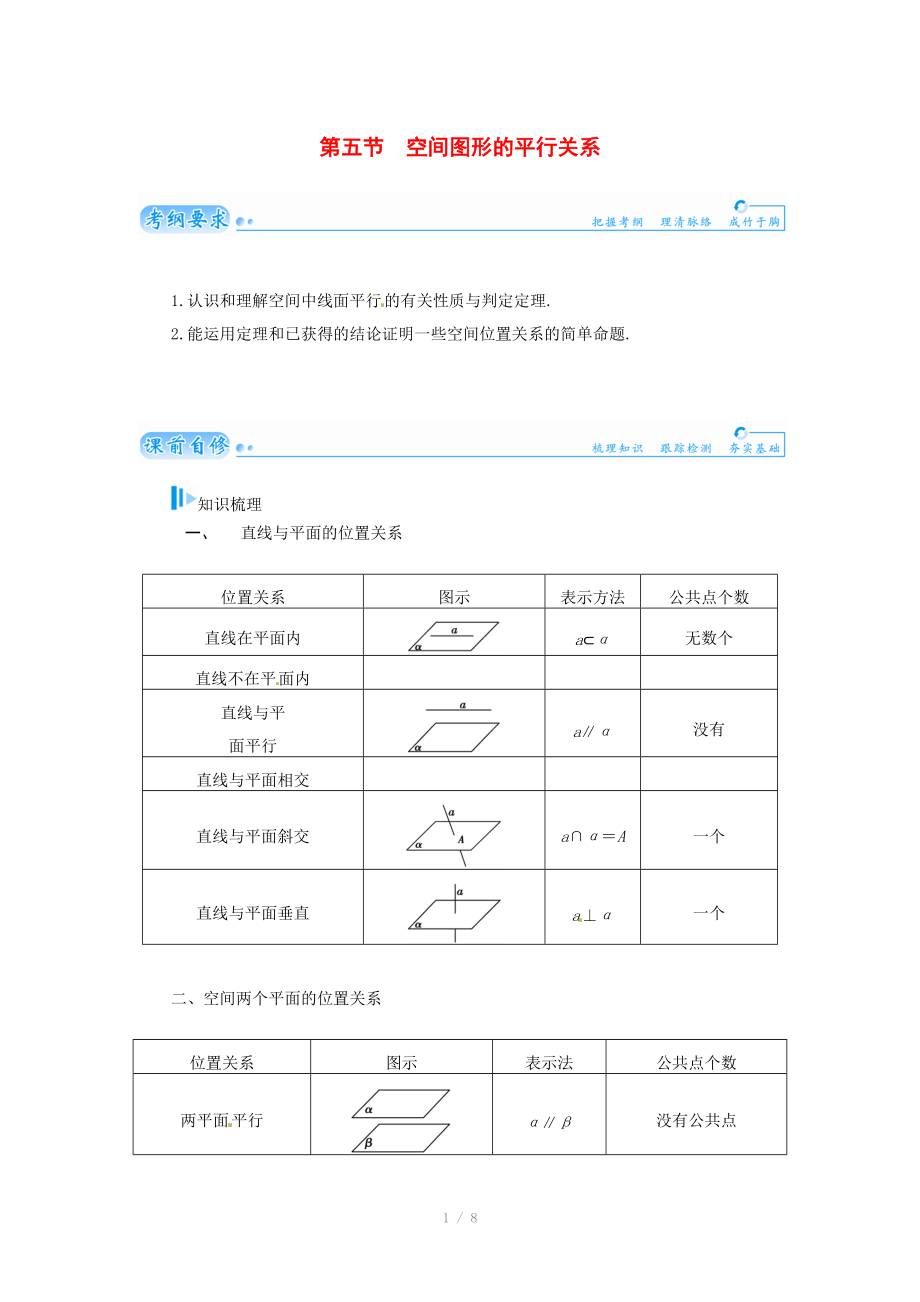
1、 第五節(jié)　空間圖形的平行關系 1.認識和理解空間中線面平行的有關性質(zhì)與判定定理. 2.能運用定理和已獲得的結(jié)論證明一些空間位置關系的簡單命題. 知識梳理 一、 直線與平面的位置關系 位置關系 圖示 表示方法 公共點個數(shù) 直線在平面內(nèi) a?α 無數(shù)個 直線不在平面內(nèi) 直線與平 面平行　 a∥α 沒有 直線與平面相交 直線與平面斜交 a∩α＝A 一個 直線與平面垂直 a⊥α 一個 二、空間兩個平面的位置關系 位置關系 圖示 表示法 公共點個數(shù) 兩平面平行 α∥β

2、 沒有公共點 1 / 8 兩平面相交 α∩β＝l 無數(shù)個 三、直線和平面平行的判定方法 四、兩個平面平行的判定 類別 語言表述 圖示 字母表示 應用 判定 如果一個平面內(nèi)有兩條相交直線都平行于另一個平面，那么這兩個平面平行 ?α∥β 證兩平面平行 如果一個平面內(nèi)有兩條相交直線分別平行于另一個平面內(nèi)的兩條直線，那么這兩個平面平行 α∥β 垂直于同一條直線的兩個平面平行 ?α∥β 五、直線與平面平行的性質(zhì) 類別 語言表述 圖示 字母表示 應用 性質(zhì) 如果一條直線和一個平面

3、平行，經(jīng)過這條直線的平面和這個平面相交，那么這條直線和交線平行 ?a∥l 證直線和直線平行 六、兩個平面平行的性質(zhì) 類別 語言表述 圖示 字母表示 應用 性質(zhì) 如果兩個平面平行，那么其中一個平面內(nèi)的直線必平行于另一個平面 ? a∥β 證直線和平面平行 如果兩個平行平面同時和第三個平面相交，那么它們的交線平行 ?a∥b 證兩條直線平行 一條直線垂直于兩個平行平面中的一個平面，它也垂直于另一個平面 ? a⊥β 證直線和平面垂直 基礎自測 1．(2013·山東省高考沖刺預測)設m，n是平面α

4、內(nèi)的兩條不同直線，l1，l2是平面β內(nèi)的兩條相交直線，則α∥β的一個充分不必要條件是(　　) A．m∥β且l1∥α B．m∥l1且n∥l2 C．m∥β且n∥β D．m∥β且n∥l2 解析：m∥l1且n∥l2，m，n?α，l1，l2為β內(nèi)兩條相交直線，則可得α∥β；若α∥β，l1，l2為β內(nèi)兩條相交直線，則不一定有m∥l1且n∥l2.故選B. 答案：B 2．(2013·肇慶二模)對于平面α和直線m，n，下列命題中假命題的個數(shù)是(　　) ①若m⊥α，m⊥n，則n∥α； ②若m∥α，n∥α，則m∥n； ③若m∥α，n?α，則m∥n； ④若m∥n，n∥α，則m∥

5、α A．1個　　　　 B．2個 C．3個 D．4個 解析：對于①，因為m⊥α，m⊥n，則n∥α或n?α，不一定得到n∥α，故①是假命題； 對于②，設正方體的上底面為α，則在下底面內(nèi)任意取兩條直線m、n，有m∥α且n∥α，但不一定有m∥n成立，故②是假命題； 對于③，設正方體的上底面為α，在下底面內(nèi)任意取直線m，則m∥α，而直線m與α內(nèi)的直線n可能平行，也可能是異面直線，不一定有m∥n成立，故③是假命題； 對于④，若m∥n，n∥α，則m∥α或m?α，不一定得到m∥α，故④是假命題． 綜上所述，可得假命題有①②③④，共4個． 答案：D 3．在正方體ABCDA1B1

6、C1D1中，E是DD1的中點，則BD1與平面ACE的位置關系為________． 解析：如圖，連接AC，BD交于點O，連接OE，因為OE∥BD1，而OE?平面ACE，BD1?平面ACE，∴BD1∥平面ACE. 答案：平行 4．設a，b，c為三條不重合的直線，α，β，γ為三個不重合的平面，直線均不在平面內(nèi)，給出六個命題： ①?a∥b； ②?a∥b； ③?α∥β； ④?a∥α； ⑤?α∥β； ⑥?a∥α. 其中正確的命題是______(將正確的序號都填上)． 答案：①④⑤⑥ 1．(2013·廣東卷)設l為直線，

7、α，β是兩個不同的平面，下列命題中正確的是(　　) A．若l∥α，l∥β，則α∥β B．若l⊥α，l⊥β，則α∥β C．若l⊥α，l∥β，則α∥β D．若α⊥β，l∥α，則l⊥β 解析：根據(jù)兩個平面平行的判定定理和面面垂直的性質(zhì)定理，易知選項A、C、D錯誤．故選B. 答案：B 2．(2013·陜西卷)如圖，四棱柱ABCD－A1B1C1D1的底面ABCD是正方形，O為底面中心，A1O⊥平面ABCD，AB＝AA1＝. (1)證明：平面A1BD//平面CD1B1； (2)求三棱柱ABD－A1B1D1的體積． (1)證明：設B1D1線段的中點為O1

8、. ∵BD和B1D1是ABCD－A1B1C1D1的對應棱， ∴BD∥B1D1. 同理，∵AO和A1O1是棱柱ABCD－A1B1C1D1的對應線段． ∴AO∥A1O1且AO∥OC?A1O1∥OC且A1O1＝OC?四邊形A1OCO1為平行四邊形?A1O∥O1C.且A1O∩BD＝O，O1C∩B1D1＝O1?面A1BD∥面CD1B1. (2)解析：∵A1O⊥面ABCD，∴A1O是三棱柱A1B1D1－ABD的高． 在正方形ABCD中，AO＝1.在Rt△A1OA中，A1O＝1， 三棱柱A1B1D1－ABD的體積VA1B1D1－ABD＝S△ABD·A1O＝×()2

9、5;1＝1. 所以，三棱柱ABD－A1B1D1的體積VA1B1C1－ABC＝1. 1．平面α∥平面β的一個充分條件是(　　) A．存在一條直線a，a∥α，a∥β B．存在一條直線a，a?α，a∥β C．存在兩條平行直線a，b，a?α，b?β，a∥β，b∥α D．存在兩條異面直線a，b，a?α，b?β，a∥β，b∥α 解析：若α∩β＝l，a∥l，a?α，α?β，a∥α，a∥β，排除選項A；若α∩β＝l，a?α，a∥l，則a∥β，選項B錯誤；若α∩β＝l，a?α，a∥l，b?β，b∥l，則a∥β，b∥α，選項C錯誤，故正確答案為選項D. 答案：D

10、2．(2013·東莞二模)如圖，在三棱柱ABC－A1B1C1中，側(cè)棱AA1⊥底面ABC，AB⊥BC，D為AC的中點，AA1＝AB＝2. (1)求證：AB1∥平面BC1D； (2)若BC＝3，求三棱錐D－BC1C的體積． (1)證明：連接B1C，設B1C與BC1相交于O，連接OD， 因為四邊形BCC1B1是平行四邊形，所以點O為B1C的中點． 因為D為AC的中點，所以OD為△AB1C的中位線，所以OD∥B1A. OD?平面BC1D，AB1?平面BC1D， 所以AB1∥平面BC1D. (2)解析：因為三棱柱ABC－A1B1C1，所以側(cè)棱CC1∥AA1， 又因為AA1⊥底面ABC，所以側(cè)棱CC1⊥底面ABC， 故CC1為三棱錐C1－BCD的高，A1A＝CC1＝2， 所以S△BCD＝S△ABC＝＝. 所以VD－BCC1＝VC1－BCD＝CC1·S△BCD＝×2×＝1. 希望對大家有所幫助，多謝您的瀏覽！